Advertisements
Advertisements
Question
Prove that `1/2 "cos"^(-1) ((1-"x")/(1+"x")) = "tan"^-1 sqrt"x"`
Solution
L.H.S. = `1/2"cos"^-1((1-"x")/(1+"x"))`
Put x = tan2θ ⇒ tan θ = `sqrt"x" => theta = "tan"^-1 sqrt"x"`
`= 1/2 "cos"^-1 ((1 - "tan"^2theta)/(1 + "tan"^2theta)) = 1/2 "cos"^-1 ("cos"2theta)`
`= 1/2 xx 2theta = theta = "tan"^-1 sqrt"x" = "R.H.S"`
APPEARS IN
RELATED QUESTIONS
Show that the function `f(x)=|x-3|,x in R` is continuous but not differentiable at x = 3.
Examine the continuity of the function f(x) = 2x2 – 1 at x = 3.
Find all points of discontinuity of f, where f is defined by `f(x) = {(x^3 - 3, if x <= 2),(x^2 + 1, if x > 2):}`
Find the points of discontinuity of f, where `f (x) = {(sinx/x, if x<0),(x + 1, if x >= 0):}`
Determine if f defined by `f(x) = {(x^2 sin 1/x, "," if x != 0),(0, "," if x = 0):}` is a continuous function?
Examine the continuity of f, where f is defined by `f(x) = {(sin x - cos x, if x != 0),(-1, "," if x = 0):}`
Find all the points of discontinuity of f defined by `f(x) = |x| - |x + 1|`.
Test the continuity of the function on f(x) at the origin:
\[f\left( x \right) = \begin{cases}\frac{x}{\left| x \right|}, & x \neq 0 \\ 1 , & x = 0\end{cases}\]
Find the points of discontinuity, if any, of the following functions: \[f\left( x \right) = \begin{cases}2x , & \text{ if } & x < 0 \\ 0 , & \text{ if } & 0 \leq x \leq 1 \\ 4x , & \text{ if } & x > 1\end{cases}\]
Find the points of discontinuity, if any, of the following functions: \[f\left( x \right) = \begin{cases}x^{10} - 1, & \text{ if } x \leq 1 \\ x^2 , & \text{ if } x > 1\end{cases}\]
Find the points of discontinuity, if any, of the following functions: \[f\left( x \right) = \begin{cases}- 2 , & \text{ if }& x \leq - 1 \\ 2x , & \text{ if } & - 1 < x < 1 \\ 2 , & \text{ if } & x \geq 1\end{cases}\]
The function f (x) = tan x is discontinuous on the set
Show that the function `f(x) = |x-4|, x ∈ R` is continuous, but not diffrent at x = 4.
If f(x) = `{{:("a"x + 1, "if" x ≥ 1),(x + 2, "if" x < 1):}` is continuous, then a should be equal to ______.
Find all points of discontinuity of the function f(t) = `1/("t"^2 + "t" - 2)`, where t = `1/(x - 1)`
`lim_("x"-> 0) sqrt(1/2 (1 - "cos" 2"x"))/"x"` is equal to
The domain of the function f(x) = `""^(24 - x)C_(3x - 1) + ""^(40 - 6x)C_(8x - 10)` is
The function f defined by `f(x) = {{:(x, "if" x ≤ 1),(5, "if" x > 1):}` discontinuous at x equal to
Sin |x| is a continuous function for
Let a, b ∈ R, b ≠ 0. Define a function
F(x) = `{{:(asin π/2(x - 1)",", "for" x ≤ 0),((tan2x - sin2x)/(bx^3)",", "for" x > 0):}`
If f is continuous at x = 0, then 10 – ab is equal to ______.
If function f(x) = `{{:((asinx + btanx - 3x)/x^3,",", x ≠ 0),(0,",", x = 0):}` is continuous at x = 0 then (a2 + b2) is equal to ______.
If functions g and h are defined as
g(x) = `{{:(x^2 + 1, x∈Q),(px^2, x\cancel(∈)Q):}`
and h(x) = `{{:(px, x∈Q),(2x + q, x\cancel(∈)Q):}`
If (g + h)(x) is continuous at x = 1 and x = 3, then 3p + q is ______.
If f(x) = `{{:((log_(sin|x|) cos^2x)/(log_(sin|3x|) cos x/2), |x| < π/3; x ≠ 0),(k, x = 0):}`, then value of k for which f(x) is continuous at x = 0 is ______.
If the function f defined as f(x) = `1/x - (k - 1)/(e^(2x) - 1)` x ≠ 0, is continuous at x = 0, then the ordered pair (k, f(0)) is equal to ______.
Find the value of k for which the function f given as
f(x) =`{{:((1 - cosx)/(2x^2)",", if x ≠ 0),( k",", if x = 0 ):}`
is continuous at x = 0.
If f(x) = `{{:((kx)/|x|"," if x < 0),( 3"," if x ≥ 0):}` is continuous at x = 0, then the value of k is ______.
The graph of the function f is shown below.
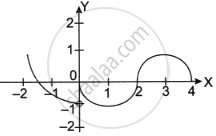
Of the following options, at what values of x is the function f NOT differentiable?
