Advertisements
Advertisements
Question
Line joining the points (3, – 4) and (– 2, 6) is perpendicular to the line joining the points (–3, 6) and (9, –18).
Options
True
False
Solution
This statement is False.
Explanation:
The given points are (3, – 4) and (– 2, 6), (– 3, 6) and (9, – 18).
Slope of the line joining the points (3, – 4) and (– 2, 6)
`m_1 = (6 + 4)/(-2 - 3)`
= `10/(-5)`
= – 2
Slope of the line joining the points (– 3, 6) and (9, – 18)
`m_2 = (-18 - 6)/(9 + 3)`
= `(-24)/12`
= – 2
Since m1 = m2 = – 2
So, the lines are parallel and not perpendicular.
APPEARS IN
RELATED QUESTIONS
Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P (0, –4) and B (8, 0).
Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (–1, –1) are the vertices of a right angled triangle.
Find the slope of a line passing through the following point:
(−3, 2) and (1, 4)
Prove that the points (−4, −1), (−2, −4), (4, 0) and (2, 3) are the vertices of a rectangle.
The slope of a line is double of the slope of another line. If tangents of the angle between them is \[\frac{1}{3}\],find the slopes of the other line.
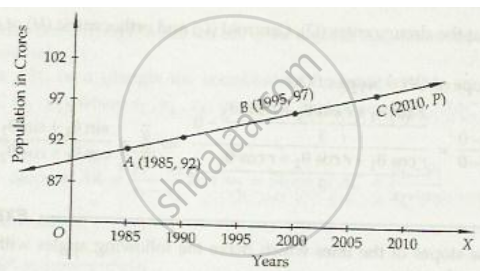
Consider the following population and year graph:
Find the slope of the line AB and using it, find what will be the population in the year 2010.
Without using the distance formula, show that points (−2, −1), (4, 0), (3, 3) and (−3, 2) are the vertices of a parallelogram.
Find the value of x for which the points (x, −1), (2, 1) and (4, 5) are collinear.
Find the equation of a straight line with slope 2 and y-intercept 3 .
Find the equations of the bisectors of the angles between the coordinate axes.
The line through (h, 3) and (4, 1) intersects the line 7x − 9y − 19 = 0 at right angle. Find the value of h.
Find the angles between the following pair of straight lines:
3x + y + 12 = 0 and x + 2y − 1 = 0
Find the acute angle between the lines 2x − y + 3 = 0 and x + y + 2 = 0.
Prove that the straight lines (a + b) x + (a − b ) y = 2ab, (a − b) x + (a + b) y = 2ab and x + y = 0 form an isosceles triangle whose vertical angle is 2 tan−1 \[\left( \frac{a}{b} \right)\].
Write the coordinates of the image of the point (3, 8) in the line x + 3y − 7 = 0.
The medians AD and BE of a triangle with vertices A (0, b), B (0, 0) and C (a, 0) are perpendicular to each other, if
The equation of the line with slope −3/2 and which is concurrent with the lines 4x + 3y − 7 = 0 and 8x + 5y − 1 = 0 is
If the line joining two points A(2, 0) and B(3, 1) is rotated about A in anticlock wise direction through an angle of 15°. Find the equation of the line in new position.
The intercept cut off by a line from y-axis is twice than that from x-axis, and the line passes through the point (1, 2). The equation of the line is ______.
The reflection of the point (4, – 13) about the line 5x + y + 6 = 0 is ______.
Find the angle between the lines y = `(2 - sqrt(3)) (x + 5)` and y = `(2 + sqrt(3))(x - 7)`
The equation of the straight line passing through the point (3, 2) and perpendicular to the line y = x is ______.
Equation of the line passing through (1, 2) and parallel to the line y = 3x – 1 is ______.
One vertex of the equilateral triangle with centroid at the origin and one side as x + y – 2 = 0 is ______.
The points A(– 2, 1), B(0, 5), C(– 1, 2) are collinear.
| Column C1 | Column C2 |
| (a) The coordinates of the points P and Q on the line x + 5y = 13 which are at a distance of 2 units from the line 12x – 5y + 26 = 0 are |
(i) (3, 1), (–7, 11) |
| (b) The coordinates of the point on the line x + y = 4, which are at a unit distance from the line 4x + 3y – 10 = 0 are |
(ii) `(- 1/3, 11/3), (4/3, 7/3)` |
| (c) The coordinates of the point on the line joining A (–2, 5) and B (3, 1) such that AP = PQ = QB are |
(iii) `(1, 12/5), (-3, 16/5)` |
