Advertisements
Advertisements
Question
Solve the equation 21x2 – 28x + 10 = 0
Solution
The given quadratic equation is 21x2 – 28x + 10 = 0
On comparing the given equation with ax2 + bx + c = 0, we obtain
a = 21, b = –28, and c = 10
Therefore, the discriminant of the given equation is
D = b2 – 4ac = (–28)2 – 4 × 21 × 10 = 784 – 840 = –56
Therefore, the required solutions are
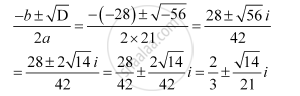
APPEARS IN
RELATED QUESTIONS
Solve the equation x2 + 3 = 0
Solve the equation x2 + 3x + 9 = 0
Solve the equation –x2 + x – 2 = 0
Solve the equation `sqrt2x^2 + x + sqrt2 = 0`
Solve the equation `x^2 + x/sqrt2 + 1 = 0`
Solve the equation 27x2 – 10x + 1 = 0
x2 + 1 = 0
4x2 − 12x + 25 = 0
\[4 x^2 + 1 = 0\]
\[5 x^2 - 6x + 2 = 0\]
\[8 x^2 - 9x + 3 = 0\]
\[\sqrt{3} x^2 - \sqrt{2}x + 3\sqrt{3} = 0\]
\[x^2 + x + \frac{1}{\sqrt{2}} = 0\]
\[3 x^2 - 4x + \frac{20}{3} = 0\]
Solving the following quadratic equation by factorization method:
\[6 x^2 - 17ix - 12 = 0\]
Solve the following quadratic equation:
\[\left( 2 + i \right) x^2 - \left( 5 - i \right) x + 2 \left( 1 - i \right) = 0\]
Solve the following quadratic equation:
\[2 x^2 + \sqrt{15}ix - i = 0\]
If roots α, β of the equation \[x^2 - px + 16 = 0\] satisfy the relation α2 + β2 = 9, then write the value P.
If \[2 + \sqrt{3}\] is root of the equation \[x^2 + px + q = 0\] than write the values of p and q.
If a and b are roots of the equation \[x^2 - x + 1 = 0\], then write the value of a2 + b2.
Write the number of quadratic equations, with real roots, which do not change by squaring their roots.
The values of x satisfying log3 \[( x^2 + 4x + 12) = 2\] are
The number of solutions of `x^2 + |x - 1| = 1` is ______.
If x is real and \[k = \frac{x^2 - x + 1}{x^2 + x + 1}\], then
The value of a such that \[x^2 - 11x + a = 0 \text { and } x^2 - 14x + 2a = 0\] may have a common root is
The number of roots of the equation \[\frac{(x + 2)(x - 5)}{(x - 3)(x + 6)} = \frac{x - 2}{x + 4}\] is
If the difference of the roots of \[x^2 - px + q = 0\] is unity, then
If α, β are the roots of the equation \[x^2 - p(x + 1) - c = 0, \text { then } (\alpha + 1)(\beta + 1) =\]
Find the value of P such that the difference of the roots of the equation x2 – Px + 8 = 0 is 2.
Find the value of a such that the sum of the squares of the roots of the equation x2 – (a – 2)x – (a + 1) = 0 is least.
