Question

The equation of the incircle formed by the coordinate axes and the line 4x + 3y = 6 is

Options

• x² + y² − 6x −6y + 9 = 0 

• 4 (x² + y² − x − y) + 1 = 0

• 4 (x² + y² + x + y) + 1 = 0

• none of these

Answer 1

 4 (x² + y² − x − y) + 1 = 0
The line 4x + 3y = 6 cuts the coordinate axes at $$(\frac{3}{2},0)\text{ and }(0,2)$$

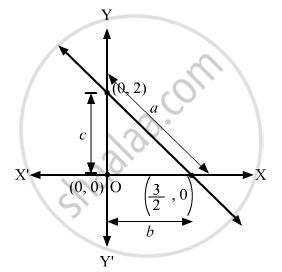
The coordinates of the incentre is

$$(\frac{a{x}_1+b{x}_2+c{x}_3}{a+b+c},\frac{a{y}_1+b{y}_2+c{y}_3}{a+b+c})$$.

Here,

$$a=\frac{5}{2},b=\frac{3}{2},c=2,x_1=0,y_1=0,x_2=0,y_2=2,x_3=\frac{3}{2},y_3=0$$

Thus, the coordinates of the incentre:

$$(\frac{0+0+3}{6},\frac{0+3+0}{6})$$

$$=(\frac{1}{2},\frac{1}{2})$$

The equation of the incircle:

$${(x-\frac{1}{2})}^2+{(y-\frac{1}{2})}^2=a^2$$

Also, radius of the incircle = $$\frac{\sqrt{s(s-a)(s-b)(s-c)}}{s}$$

Here, $$s=\frac{a+b+c}{2}=\frac{\frac{5}{2}+\frac{3}{2}+2}{2}=3$$

∴ Radius of the incircle = $$\frac{\sqrt{3(3-a)(3-b)(3-c)}}{3}$$

$$=\frac{\sqrt{3(3-\frac{5}{2})(3-\frac{3}{2})(3-2)}}{3}$$

$$=\frac{\sqrt{3\left(\frac{1}{2}\right)\left(\frac{3}{2}\right)}}{3}$$

$$=\frac{1}{2}$$

The equation of circle: $${(x-\frac{1}{2})}^2+{(y-\frac{1}{2})}^2=\frac{1}{4}$$

$$\Rightarrow 4(x^2+y^2-x-y)+1=0$$