Advertisements
Advertisements
Question
Without using distance formula, show that points (–2, –1), (4, 0), (3, 3) and (–3, 2) are vertices of a parallelogram.
Solution
Let the vertices of a quadrilateral be A(−2, –1), B(4, 0), C(3, 3), and D(−3, 2).
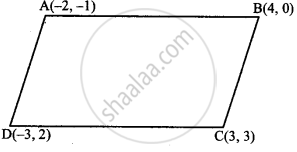
Slope of AB = `("y"_2 - "y"_1)/("x"_2 - "x"_1)`
= `(0 + 1)/(4 + 2)`
= `1/6`
Slope of DC = `(3 - 2)/(3 + 3)`
= `1/6`
Slope of AB = Slope of DC
That means AB || DC
Slope of BC = `(3 - 0)/(3 - 4)`
= `3/(-1)`
= −3
Slope of AD = `(2 + 1)/(-3 + 2)`
= `3/(-1)`
= −3
∴ Slope of BC = Slope of AD
That means BC || AD
Hence, AB || DC, BC || AD
Hence, ABCD is a parallelogram.
APPEARS IN
RELATED QUESTIONS
Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (–1, –1) are the vertices of a right angled triangle.
Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
Find the equation of a line drawn perpendicular to the line `x/4 + y/6 = 1`through the point, where it meets the y-axis.
State whether the two lines in each of the following are parallel, perpendicular or neither.
Through (9, 5) and (−1, 1); through (3, −5) and (8, −3)
Find the slope of a line (i) which bisects the first quadrant angle (ii) which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
What can be said regarding a line if its slope is zero ?
What can be said regarding a line if its slope is positive ?
What can be said regarding a line if its slope is negative?
Show that the line joining (2, −3) and (−5, 1) is parallel to the line joining (7, −1) and (0, 3).
Without using Pythagoras theorem, show that the points A (0, 4), B (1, 2) and C (3, 3) are the vertices of a right angled triangle.
Prove that the points (−4, −1), (−2, −4), (4, 0) and (2, 3) are the vertices of a rectangle.
Without using the distance formula, show that points (−2, −1), (4, 0), (3, 3) and (−3, 2) are the vertices of a parallelogram.
By using the concept of slope, show that the points (−2, −1), (4, 0), (3, 3) and (−3, 2) are the vertices of a parallelogram.
Find the equations of the bisectors of the angles between the coordinate axes.
Find the equation of the strainght line intersecting y-axis at a distance of 2 units above the origin and making an angle of 30° with the positive direction of the x-axis.
Find the coordinates of the orthocentre of the triangle whose vertices are (−1, 3), (2, −1) and (0, 0).
Find the equations of the altitudes of a ∆ ABC whose vertices are A (1, 4), B (−3, 2) and C (−5, −3).
Find the equation of the right bisector of the line segment joining the points (3, 4) and (−1, 2).
Find the angles between the following pair of straight lines:
3x − y + 5 = 0 and x − 3y + 1 = 0
Prove that the points (2, −1), (0, 2), (2, 3) and (4, 0) are the coordinates of the vertices of a parallelogram and find the angle between its diagonals.
Find the angle between the line joining the points (2, 0), (0, 3) and the line x + y = 1.
The medians AD and BE of a triangle with vertices A (0, b), B (0, 0) and C (a, 0) are perpendicular to each other, if
The coordinates of the foot of the perpendicular from the point (2, 3) on the line x + y − 11 = 0 are
The equation of a line passing through the point (7, - 4) and perpendicular to the line passing through the points (2, 3) and (1 , - 2 ) is ______.
If x + y = k is normal to y2 = 12x, then k is ______.
The equation of the line passing through (1, 2) and perpendicular to x + y + 7 = 0 is ______.
The coordinates of the foot of the perpendicular from the point (2, 3) on the line x + y – 11 = 0 are ______.
Find the equation of a straight line on which length of perpendicular from the origin is four units and the line makes an angle of 120° with the positive direction of x-axis.
P1, P2 are points on either of the two lines `- sqrt(3) |x|` = 2 at a distance of 5 units from their point of intersection. Find the coordinates of the foot of perpendiculars drawn from P1, P2 on the bisector of the angle between the given lines.
If p is the length of perpendicular from the origin on the line `x/a + y/b` = 1 and a2, p2, b2 are in A.P, then show that a4 + b4 = 0.
The equation of the straight line passing through the point (3, 2) and perpendicular to the line y = x is ______.
The tangent of angle between the lines whose intercepts on the axes are a, – b and b, – a, respectively, is ______.
Equations of diagonals of the square formed by the lines x = 0, y = 0, x = 1 and y = 1 are ______.
One vertex of the equilateral triangle with centroid at the origin and one side as x + y – 2 = 0 is ______.
The points A(– 2, 1), B(0, 5), C(– 1, 2) are collinear.
The line `x/a + y/b` = 1 moves in such a way that `1/a^2 + 1/b^2 = 1/c^2`, where c is a constant. The locus of the foot of the perpendicular from the origin on the given line is x2 + y2 = c2.
The three straight lines ax + by = c, bx + cy = a and cx + ay = b are collinear, if ______.
