Advertisements
Advertisements
Question
Write a condition under which a bimolecular reaction is kinetically first order. Give an example of such a reaction. (Given : log2 = 0.3010,log 3 = 0.4771, log5 = 0.6990).
Solution
\[\ce{ C_12 H22O11 + H2O ->[H+] C6 + \underset{Glucose}{C6H12O6} + \underset{Fructose}{C6H12O6} }\] Rate=K[C12H22O4]
Biomolecular reaction is Kinetically first order. Consider a chemical reaction between two substances when one reactanct is present in large excess.
`CH_3 COOC_2H5 +H_2O -> CH_3OOH + C_2H_5OH`
t=0 0.01mol 10mol 0 0
t 0mol 9.9mol 0.01 0.01 mol
Rate = K[CH3COOC2H5]
`Rate = K[CH_3COOC_2H_5] where K=K' [H2O]` the reaction behaves as first order reactions.
APPEARS IN
RELATED QUESTIONS
(b) Rate constant ‘k’ of a reaction varies with temperature ‘T’ according to the equation:
`logk=logA-E_a/2.303R(1/T)`
Where Ea is the activation energy. When a graph is plotted for `logk Vs. 1/T` a straight line with a slope of −4250 K is obtained. Calculate ‘Ea’ for the reaction.(R = 8.314 JK−1 mol−1)
The rate constant for the first-order decomposition of H2O2 is given by the following equation:
`logk=14.2-(1.0xx10^4)/TK`
Calculate Ea for this reaction and rate constant k if its half-life period be 200 minutes.
(Given: R = 8.314 JK–1 mol–1)
The rate constant for the decomposition of N2O5 at various temperatures is given below:
| T/°C | 0 | 20 | 40 | 60 | 80 |
| 105 × k/s−1 | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
Draw a graph between ln k and `1/"T"` and calculate the values of A and Ea. Predict the rate constant at 30º and 50ºC.
Consider figure and mark the correct option.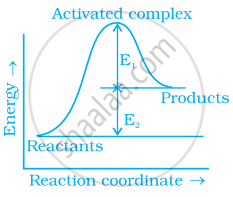
Which of the following statements are in accordance with the Arrhenius equation?
(i) Rate of a reaction increases with increase in temperature.
(ii) Rate of a reaction increases with decrease in activation energy.
(iii) Rate constant decreases exponentially with increase in temperature.
(iv) Rate of reaction decreases with decrease in activation energy.
The reaction between \[\ce{H2(g)}\] and \[\ce{O2(g)}\] is highly feasible yet allowing the gases to stand at room temperature in the same vessel does not lead to the formation of water. Explain.
Oxygen is available in plenty in air yet fuels do not burn by themselves at room temperature. Explain.
In respect of the eqn k = \[\ce{Ae^{{-E_a}/{RT}}}\] in chemical kinetics, which one of the following statement is correct?
The equation k = `(6.5 xx 10^12 "s"^(-1))"e"^(- 26000 " K"//"T")` is followed for the decomposition of compound A. The activation energy for the reaction is ______ kJ mol-1. (Nearest integer) (Given: R = 8.314 JK-1 mol-1)
It is generally observed that the rate of a chemical reaction becomes double with every 10oC rise in temperature. If the generalisation holds true for a reaction in the temperature range of 298K to 308K, what would be the value of activation energy (Ea) for the reaction?
