Advertisements
Advertisements
Question
The rate constant for the decomposition of N2O5 at various temperatures is given below:
| T/°C | 0 | 20 | 40 | 60 | 80 |
| 105 × k/s−1 | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
Draw a graph between ln k and `1/"T"` and calculate the values of A and Ea. Predict the rate constant at 30º and 50ºC.
Solution
The rate constants for the decomposition of N2O5 at different temperatures are shown below.
| T(°C) | T(K) | 1/T | k(s−1) | In k (= 2.303 log k) |
| 0 | 273 | 3.6 × 10−3 | 7.87 × 10−7 | −14.06 |
| 20 | 293 | 3.4× 10−3 | 1.70 × 10−5 | −10.98 |
| 40 | 313 | 3.19 × 10−3 | 25.7 × 10−5 | −8.266 |
| 60 | 333 | 3.00 × 10−3 | 178 × 10−5 | −6.332 |
| 80 | 353 | 2.8 × 10−3 | 2140 × 10−5 | −3.844 |
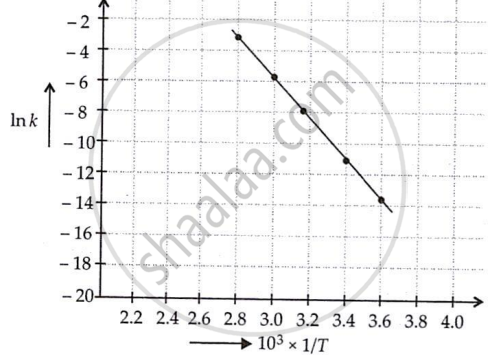
Slope of the line = tan θ
= `("y"_2 - "y"_1)/("x"_2 - "x"_1)`
= `(-10.98-(-14.06))/(3.4 - 3.6) xx 10^3`
= −15.5 × 103
Ea = −slope × R
= −(−15.5 × 103 × 8.314)
= 128.86kJ K−1 mol−1
Again In A = In k + `"E"_"a"/("RT")`
= `-14.06 + (128.86 xx 10^3 "JK"^(-1) "mol"^(-1))/(8.314 xx 273)`
= −14.06 + 56.77
= 42.71
or, log A = 18.53
or, A = antilog 18.53 = 0.3388 × 1019
or, A = 3.3888 × 1018
Values of rate constant k at 303 K and 323 K can be obtained from the graph.
First, k is obtained corresponding to `1/(303"K") and 1/(323"K")` and then k is calculated.
APPEARS IN
RELATED QUESTIONS
(b) Rate constant ‘k’ of a reaction varies with temperature ‘T’ according to the equation:
`logk=logA-E_a/2.303R(1/T)`
Where Ea is the activation energy. When a graph is plotted for `logk Vs. 1/T` a straight line with a slope of −4250 K is obtained. Calculate ‘Ea’ for the reaction.(R = 8.314 JK−1 mol−1)
The activation energy for the reaction \[\ce{2 HI_{(g)} -> H2_{(g)} + I2_{(g)}}\] is 209.5 kJ mol−1 at 581K. Calculate the fraction of molecules of reactants having energy equal to or greater than activation energy?
The decomposition of A into product has value of k as 4.5 × 103 s−1 at 10°C and energy of activation 60 kJ mol−1. At what temperature would k be 1.5 × 104 s−1?
In the Arrhenius equation for a first order reaction, the values of ‘A’ of ‘Ea’ are 4 x 1013 sec-1 and 98.6 kJ mol-1 respectively. At what temperature will its half life period be 10 minutes?
[R = 8.314 J K-1 mol-1]
The rate constant of a first order reaction are 0.58 S-1 at 313 K and 0.045 S-1 at 293 K. What is the energy of activation for the reaction?
Calculate activation energy for a reaction of which rate constant becomes four times when temperature changes from 30 °C to 50 °C. (Given R = 8.314 JK−1 mol−1).
A first-order reaction is 50% completed in 40 minutes at 300 K and in 20 minutes at 320 K. Calculate the activation energy of the reaction. (Given : log 2 = 0·3010, log 4 = 0·6021, R = 8·314 JK–1 mol–1)
Explain the following terms :
Half life period of a reaction (t1/2)
The decomposition of a hydrocarbon has value of rate constant as 2.5×104s-1 At 27° what temperature would rate constant be 7.5×104 × 3 s-1if energy of activation is 19.147 × 103 J mol-1 ?
Predict the main product of the following reactions: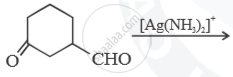
The chemical reaction in which reactants require high amount of activation energy are generally ____________.
The rate of chemical reaction becomes double for every 10° rise in temperature because of ____________.
Consider figure and mark the correct option.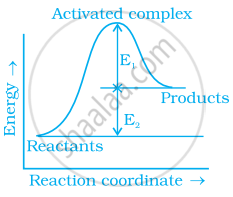
Which of the following graphs represents exothermic reaction?
(a)
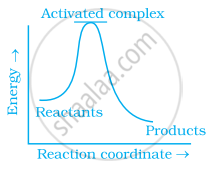
(b)
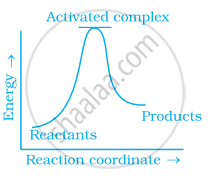
(c)
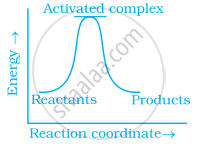
Oxygen is available in plenty in air yet fuels do not burn by themselves at room temperature. Explain.
Thermodynamic feasibility of the reaction alone cannot decide the rate of the reaction. Explain with the help of one example.
The activation energy in a chemical reaction is defined as ______.
What happens to the rate constant k and activation energy Ea as the temperature of a chemical reaction is increased? Justify.
