Mathematics Delhi Set - 1 2023-2024 Commerce (English Medium) Class 12 Question Paper Solution

A function f: `RR → RR` defined as f(x) = x² − 4x + 5 is: 

injective but not surjective

surjective but not injective

both injective and surjective

neither injective nor surjective

If A = `[(a, c, -1),(b, 0, 5),(1, -5, 0)]` is a skew-symmetric matrix, then the value of 2a − (b + c) is _______.

0

1

−10

10

If A is a square matrix of order 3 such that the value of |adj. A| = 8, then the value of |A^T| is ________.

`sqrt2`

`-sqrt2`

8

`2sqrt2`

If inverse of matrix `[(7, -3, -3),(-1, 1, 0),(-1, 0, 1)]` is the matrix `[(1, 3, 3),(1, lambda, 3),(1, 3, 4)]`, then value of λ is ______.

−4

1

3

4

If `[x   2   0] [(5),(-1),(x)] = [3  1] [(-2),(x)]`, then value of x is ______.

−1

0

1

2

Find the matrix A², where A = [a_ij] is a 2 × 2 matrix whose elements are given by a_ij = maximum (i, j) − minimum (i, j): 

`[(0, 0),(0, 0)]`

`[(0, 1),(1, 0)]`

`[(1, 0),(0, 1)]`

`[(1, 1),(1, 1)]`

If xe^y = 1, then the value of `dy/dx` at x = 1 is ______.

−1

1

−e

`-1/e`

Derivative of `e^(sin^2x)` with respect to cos x is ______.

`sin x  e^(sin^2x)`

`cos x  e^(sin^2x)`

`−2 cos x  e^(sin^2x)`

`−2 sin^2 x cos x  e^(sin^2x)`

The function f(x) = `x/2 + 2/x` has a local minima at x equal to ______.

2

1

0

−2

Given a curve y = 7x − x³ and x increases at the rate of 2 units per second. The rate at which the slope of the curve is changing, when x = 5 is ______.

−60 units/sec

60 units/sec

−70 units/sec

−140 units/sec

`int 1/(x(log x)^2) dx` is equal to ______.

2 log (log x) + c

`-1/(log x) + c`

`(log x)^3/3 + c`

`3/(log x)^3 + c`

The value of `int_-1^1 x  |  x  |  dx` is ______.

`1/6`

`1/3`

`-1/6`

0

Area of the region bounded by curve y² = 4x and the X-axis between x = 0 and x = 1 is ______.

`2/3`

`8/3`

3

`4/3`

The order of the differential equation `(d^4y)/(dx^4) - sin[(d^2y)/(dx^2)]` = 5 is ______.

4

3

2

not defined

The position vectors of points P and Q are `overset->p and overset->q` respectively. The point R divides line segment PQ in the ratio 3 : 1 and S is the mid-point of line segment PR. The position vector of S is ______.

`(overset->p + 3overset->q)/4`

`(overset->p + 3overset->q)/8`

`(5overset->p + 3overset->q)/4`

`(5overset->p + 3overset->q)/8`

The angle which the line `x/1 = y/-1 = z/0` makes with the positive direction of Y-axis is ______.

`(5pi)/6`

`(3pi)/4`

`(5pi)/4`

`(7pi)/4`

The Cartesian equation of the line passing through the point (1, −3, 2) and parallel to the line:

`overset->r = (2 + lambda)hat i + lambda hat j + (2 lambda - 1) hat k` is:

`(x -1)/2 = (y + 3)/0 = (z - 2)/-1`

`(x +1)/1 = (y - 3)/1 = (z + 2)/2`

`(x +1)/2 = (y - 3)/0 = (z + 2)/-1`

`(x -1)/1 = (y + 3)/1 = (z - 2)/2`

If A and B are events such that P(A/B) = P(B/A) ≠ 0, then _______.

A ⊂ B, but A ≠ B

A = B

A ∩ B = Φ 

P(A) = P(B)

Assertion (A): Domain of y = cos⁻¹ (x) is [−1, 1].

Reason (R): The range of the principal value branch of y = cos⁻¹ (x) is [0, π] − `{pi/2}`.

Both Assertion (A) and Reason (R) are true and the Reason (R) is the correct explanation of the Assertion (A).

Both Assertion (A) and Reason (R) are true and Reason (R) is not the correct explanation of the Assertion (A).

Assertion (A) is true, but Reason (R) is false.

Assertion (A) is false, but Reason (R) is true.

Assertion (A): The vectors

`overset->a = 6hat i + 2 hat j - 8 hat k`

`overset->b = 10 hat i - 2 hatj - 6 hat k`

`overset ->c = 4 hat i - 4 hat j + 2 hat k`

Reason (R): Three non-zero vectors of which none of two are collinear forms a triangle if their resultant is zero vector or sum of any two vectors is equal to the third. 

Both Assertion (A) and Reason (R) are true and the Reason (R) is the correct explanation of the Assertion (A).

Both Assertion (A) and Reason (R) are true and Reason (R) is not the correct explanation of the Assertion (A).

Assertion (A) is true, but Reason (R) is false.

Assertion (A) is false, but Reason (R) is true.

Find value of k if `sin^-1 [k tan (2cos^-1  (sqrt3)/(2))] = pi/3`.

Verify whether the function f defined by f(x) = `{(x sin (1/x)",", x ≠ 0), (0",", x = 0):}`  is continuous at x = 0 or not. 

Check for differentiability of the function f defined by f(x) = |x − 5|, at the point x = 5.

The area of the circle is increasing at a uniform rate of 2 cm²/sec. How fast is the circumference of the circle increasing when the radius r = 5 cm?

Find: `int cos^3 x  e^(log sin x)  dx` 

Find: `int 1/ (5 + 4x - x^2) dx`

Find the vector equation of the line passing through the point (2, 3, −5) and making equal angles with the co-ordinate axes. 

Find `(dy)/(dx)`, if (cos x)^y = (cos y)^x. 

If `sqrt(1-x^2)  + sqrt(1- y^2)` =  a(x − y), show that dy/dx = `sqrt((1-y^2)/(1-x^2))`

If x = a sin³ θ, y = b cos³ θ, then find `(d^2y)/dx^2` at θ = `(pi)/4`.

Evaluate: `int_0^pi e^cosx/(e^cos x + e^-cos x) dx`

Find: `int (2x + 1)/((x + 1)^2(x - 1)) dx`

Find the particular solution of the differential equation `(dy)/(dx) - 2xy = 3x^2 e^(x^2); y(0) = 5`. 

Solve the following differential equation:

x² dy + y(x + y) dx = 0

Find a vector of magnitude 4 units perpendicular to each of the vectors `2hat i - hat j + hat k and hat i + hat j - hat k`  and hence verify your answer.

The random variable X has the following probability distribution where a and b are some constants:

If the mean E(X) = 3, then find values of a and b and hence determine P(X ≥ 3).

If A = `[(1, 2, -3),(2, 0, -3),(1, 2, 0)]`, then find A⁻¹ and hence solve the following system of equations: 

x + 2y − 3z = 1

2x − 3z = 2

x + 2y = 3

Find the product of the matrices `[(1, 2, -3),(2, 3, 2),(3, -3, -4)][(-6, 17, 13),(14, 5, -8),(-15, 9, -1)]` and hence solve the system of linear equations:

x + 2x − 3z = −4

2x + 3y + 2z = 2

3x − 3y − 4z = 11 

Find the area of the region bounded by the curve 4x² + y² = 36 using integration. 

Find the co-ordinates of the foot of the perpendicular drawn from the point (2, 3, −8) to the line `(4 - x)/(2) = y/6 = (1 - z)/(3)`.

Also, find the perpendicular distance of the given point from the line. 

Find the shortest distance between the lines L₁ & L₂ given below: 

L₁: The line passing through (2, −1, 1) and parallel to `x/1 = y/1 = z/3`

L₂:  `overset->r = hat i + (2mu + 1) hat j - (mu + 2) hat k`.

Solve the following L.P.P. graphically:

Maximize Z = 60x + 40y
Subject to x + 2y ≤ 12
2x + y ≤ 12
4x + 5y ≥ 20
x, y ≥ 0

Students of a school are taken to a railway museum to learn about railways heritage and its history. 

An exhibit in the museum depicted many rail lines on the track near the railway station. Let L be the set of all rail lines on the railway track and R be the relation on L defined by

R = `{(l_1, l_2) : l_1  "is parallel to"  l_2}` 

On the basis of the above information, answer the following questions:

1. Find whether the relation R is symmetric or not.
2. Find whether the relation R is transitive or not.
3. If one of the rail lines on the railway track is represented by the equation y = 3x + 2, then find the set of rail lines in R related to it. 

Let S be the relation defined by S = {(l₁, l₂) : l₁ is perpendicular to l₂} check whether the relation S is symmetric and transitive. 

A rectangular visiting card is to contain 24 sq. cm. of printed matter. The margins at the top and bottom of the card are to be 1 cm and the margins on the left and right are to be 1½ cm as shown below:

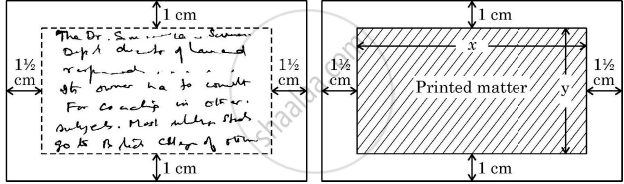
On the basis of the above information, answer the following questions:

1. Write the expression for the area of the visiting card in terms of x.
2. Obtain the dimensions of the card of minimum area.

A departmental store sends bills to charge its customers once a month. Past experience shows that 70% of its customers pay their first month bill in time. The store also found that the customer who pays the bill in time has the probability of 0.8 of paying in time next month and the customer who doesn't pay in time has the probability of 0.4 of paying in time the next month.

Based on the above information, answer the following questions:

1. Let E₁ and E₂ respectively denote the event of customer paying or not paying the first month bill in time.
   Find P(E₁), P(E₂).
2. Let A denotes the event of customer paying second month’s bill in time, then find P(A|E₁) and P(A|E₂).
3. Find the probability of customer paying second month's bill in time.
                                            OR
   Find the probability of customer paying first month’s bill in time if it is found that customer has paid the second month’s bill in time.