Advertisements
Advertisements
For the curve y2 = 2x3 – 7, the slope of the normal at (2, 3) is ______.
Concept: Tangents and Normals
The intevral in which the function f(x) = 5 + 36x – 3x2 increases will be ______.
Concept: Increasing and Decreasing Functions
A running track of 440 m is to be laid out enclosing a football field. The football field is in the shape of a rectangle with a semi-circle at each end. If the area of the rectangular portion is to be maximum,then find the length of its sides. Also calculate the area of the football field.
Concept: Maxima and Minima
In which one of the following intervals is the function f(x) = x3 – 12x increasing?
Concept: Increasing and Decreasing Functions
Given that `1/y + 1/x = 1/12` and y decreases at a rate of 1 cms–1, find the rate of change of x when x = 5 cm and y = 1 cm.
Concept: Rate of Change of Bodies or Quantities
Mrs. Roy designs a window in her son’s study room so that the room gets maximum sunlight. She designs the window in the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 m, find the dimensions of the window that will admit maximum sunlight into the room.
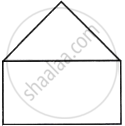
Concept: Maxima and Minima
Sumit has bought a closed cylindrical dustbin. The radius of the dustbin is ‘r' cm and height is 'h’ cm. It has a volume of 20π cm3.
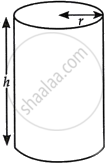
- Express ‘h’ in terms of ‘r’, using the given volume.
- Prove that the total surface area of the dustbin is `2πr^2 + (40π)/r`
- Sumit wants to paint the dustbin. The cost of painting the base and top of the dustbin is ₹ 2 per cm2 and the cost of painting the curved side is ₹ 25 per cm2. Find the total cost in terms of ‘r’, for painting the outer surface of the dustbin including the base and top.
- Calculate the minimum cost for painting the dustbin.
Concept: Maxima and Minima
Find the interval in which the function f(x) = x2e–x is strictly increasing or decreasing.
Concept: Increasing and Decreasing Functions
Find the equation to the tangent at (0, 0) on the curve y = 4x2 – 2x3
Concept: Tangents and Normals
A kite is being pulled down by a string that goes through a ring on the ground 8 meters away from the person pulling it. If the string is pulled in at 1 meter per second, how fast is the kite coming down when it is 15 meters high?
Concept: Rate of Change of Bodies or Quantities
Evaluate : `int_0^4(|x|+|x-2|+|x-4|)dx`
Concept: Evaluation of Definite Integrals by Substitution
Find : `int((2x-5)e^(2x))/(2x-3)^3dx`
Concept: Methods of Integration: Integration by Substitution
Evaluate :
`int_e^(e^2) dx/(xlogx)`
Concept: Evaluation of Definite Integrals by Substitution
Find the following integrals:
`int (x^3 - x^2 + x - 1)/(x - 1) dx`
Concept: Integration as an Inverse Process of Differentiation
By using the properties of the definite integral, evaluate the integral:
`int_0^(pi/4) log (1+ tan x) dx`
Concept: Properties of Definite Integrals
By using the properties of the definite integral, evaluate the integral:
`int_0^(pi/2) (sin x - cos x)/(1+sinx cos x) dx`
Concept: Properties of Definite Integrals
Evaluate `int(x^3+5x^2 + 4x + 1)/x^2 dx`
Concept: Integration as an Inverse Process of Differentiation
Evaluate `int tan^(-1) sqrtx dx`
Concept: Integration as an Inverse Process of Differentiation
Evaluate `int (x-1)/(sqrt(x^2 - x)) dx`
Concept: Methods of Integration: Integration by Substitution
Evaluate `int_0^(pi/2) cos^2x/(1+ sinx cosx) dx`
Concept: Properties of Definite Integrals
