Advertisements
Advertisements
ΔABC में, ∠ABC = 90°, ∠BAC = ∠BCA = 45°. यदि AC = `9sqrt(2)` हो, तो AB का मान ज्ञात करो।
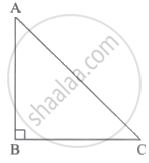
Concept: पायथागोरस के प्रमेय का विलोम
दी गई आकृति में, □ABCD एक आयत है। यदि AB = 5, AC = 13 हो, तो BC ज्ञात करने के लिए निम्न कृति पूर्ण करों:
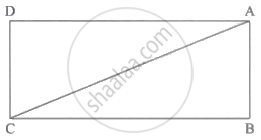
कृति: ΔABC यह `square` त्रिभुज है।
पायथागोरस प्रमेय से,
AB2 + BC2 + AC2
25 + BC2 = `square`
∴ BC2 = `square`
∴ BC = `square`
Concept: पायथागोरस के प्रमेय का विलोम
ΔABC में AB = 9 सेमी, BC = 40 सेमी, AC = 41 सेमी। स्पष्ट करो कि ΔABC समकोण त्रिभुज है या नहीं? कारण लिखो।
Concept: पायथागोरस के प्रमेय का विलोम
a तथा b प्राकृत संख्याएँ हैं। (a > b). यदि (a2 + b2), (a2 – b2) तथा 2ab त्रिभुज की भुजाएँ हैं, तो सिद्ध करो कि यह त्रिभुज समकोण त्रिभुज है। a तथा b के योग्य मान लेकर, पायथागोरस त्रिक की दो जोड़ियाँ ज्ञात करो।
Concept: पायथागोरस के त्रिक्
यदि a, b, c त्रिभुज की भुजाएँ हैं और a2 + b2 = c2 हो, तो उस त्रिभुज के प्रकार का नाम लिखिए?
Concept: पायथागोरस का प्रमेय (Theorem of Pythagoras)
∆RST में, ∠S = 90°, ∠T = 30°, RT = 12 सेमी, तो RS का मान ज्ञात कीजिए।
Concept: 30°-60°-90° माप वाले त्रिभुज का गुणधर्म
ΔPQR में, रेख PM माध्यिका है PM = 9 और PQ2 + PR2 = 290 हो, तो QR ज्ञात कीजिए।
Concept: अपोलोनियस का प्रमेय (Appollonius’ Theorem)
यदि वर्ग के विकर्ण की लंबाई 10`sqrt2` सेमी हो, तो उस वर्ग की भुजा की लंबाई ज्ञात कीजिए।
Concept: पायथागोरस का प्रमेय (Theorem of Pythagoras)
आकृति में, C केंद्रवाले वृत्त पर G, D, E और F बिंदु हैं। ∠ECF का माप 70° और चाप DGF का माप 200° हो, तो चाप DE और चाप DEF के माप ज्ञात कीजिए।
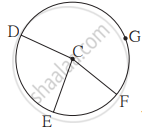
Concept: वृत्त चाप (Arc of a Circle)
आकृति में m(चाप NS) = 125°, m(चाप EF) = 37°, तो ∠NMS का माप ज्ञात कीजिए।
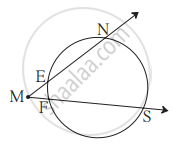
Concept: स्पर्श वृत्त (Touching Circle)
यदि ΔABC ∼ ΔDEF तथा ∠A = 48° हो, तो ∠D = ______.
Concept: स्पर्श वृत्त प्रमेय (Theorem of Touching Circles)
‘O’ केंद्रवाले वृत्त के बाह्य बिंदु ‘P’ से वृत्त पर स्थित बिंदु A से स्पर्श रेखा AP खींची गई है। OP = 12 सेमी तथा ∠OPA = 30° हो, तो वृत्त की त्रिज्या ______ होगी।
Concept: स्पर्शरेखाखंड का प्रमेय (Tangent Segment Theorem)
जीवा AB तथा जीवा CD, ‘O’ केंद्रवाले वृत्त की सर्वागसम जीवाएँ हैं। यदि m(चाप AB) = 120° हो, तो m(चाप CD) ज्ञात करो।
Concept: चाप के मापों के योग का गुणधर्म (Property of Sum of Measures of Arcs)
दी गई आकृति में, m(चाप DXE) = 105°, m(चाप AYC) = 47° हो, तो ∠DBE का मान ज्ञात करो।
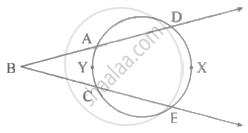
Concept: जीवाओं का अंतःछेदन प्रमेय (Theorem of Internal Division of Chords)
दी गई आकृति में, जीवा PQ तथा जीवा RS एक-दूसरे को बिंदु T पर प्रतिच्छेदित करती हैं। यदि ∠STQ = 58° तथा ∠PSR = 24° हो, ही तो निम्न कृति पूर्ण करके सिद्ध करो:
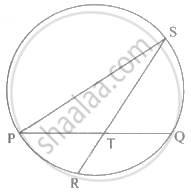
∠STQ = `1/2` [m(चाप PR) + m(चाप SQ)]
कृति: ΔPTS में,
∠STQ = ∠STQ – `square` ...(बहिष्कोण प्रमेय)
∠SPQ = 34°
m(चाप QS) = 2 × `square`° = 68° ..........(`square`)
उसी प्रकार, m(चाप PR) = 2∠PSR = `square`
`1/2` [m(चाप PR) + m(चाप PR)] = `1/2` × `square` = 58° ..........(1)
परंतु, ∠STQ = 58° .............. (2) (दिया है।)
∴ `1/2` [m(चाप PR) + m(चाप QS)] = ∠______ ...........[(1) तथा (2) से]
Concept: अंतर्लिखित कोण का प्रमेय
सिद्ध करो: ''चक्रीय चतुर्भुज के सम्मुख कोण परस्पर संपूरक होते हैं।''
Concept: चक्रीय चतुर्भुज का प्रमेय (Theorem of Cyclic Quadrilateral)
दी गई आकृति में, C केंद्रवाले वृत्त के बाह्य बिंदु A से खींची गई स्पर्श रेखाएँ AB तथा AD हैं। सिद्ध करो कि: ∠A = `1/2` [m(चाप BYD – m(चाप BXD)]
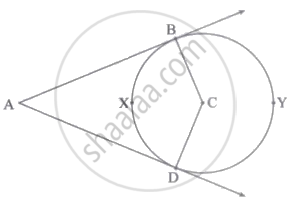
Concept: स्पर्शरेखा-त्रिज्या प्रमेय (Tangent Theorem)
केंद्र ‘O’ तथा 3 सेमी तथा 5 सेमी त्रिज्या लेकर दो एककेंद्रीय वृत्त खींचो। बड़े वृत्त पर स्थित बिंदु A से छोटे वृत्त पर स्पर्श रेखा खींचो। स्पर्श रेखाखंड की लंबाई मापकर लिखो। पायथागोरस प्रमेय का उपयोग करके स्पर्श रेखाखंड की लंबाई ज्ञात करो।
Concept: स्पर्श रेखा - त्रिज्या प्रमेय का विलोम
वृत्त को जीवाएँ AB तथा CD वृत्त के अंत:भाग में बिदु E पर प्रतिच्छेदित करती हैं। यदि AE = 4, EB = 10, CE = 8, तो ED का मान ज्ञात कीजिए?
Concept: जीवाओं का अंतःछेदन प्रमेय (Theorem of Internal Division of Chords)
यदि वृत्त की त्रिज्या 5 सेमी हो, तो उस वृत्त की सबसे बड़ी जीवा की लंबाई ज्ञात कीजिए।
Concept: वृत्त
