SSC (English Medium) 10th Standard Board Exam - Maharashtra State Board Question Bank Solutions for Geometry Mathematics 2

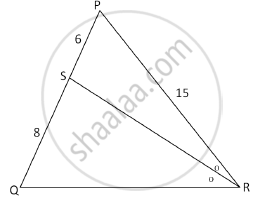
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.

ΔSHR ~ ΔSVU. In ΔSHR, SH = 4.5 cm, HR = 5.2 cm, SR = 5.8 cm and `"SH"/("SV")=3/5`. Construct ΔSVU.

Draw ∠ABC of measure 105° and bisect it.

In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.

PS = 3, SQ = 9, PR = 18. Find QR.

Prove that the angle bisector of a triangle divides the side opposite to the angle in the ratio of the remaining sides.

In the figure given below, Ray PT is bisector of ∠QPR. If PQ = 5.6 cm, QT = 4 cm and TR = 5 cm, find the value of x .

In a triangle ABC, line l || Side BC and line l intersects side AB and AC in points P and Q, respectively. Prove that: `"AP"/"BP"="AQ"/"QC"`

Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right-angled isosceles triangle.

In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that

(i) ΔPAC ∼ ΔPDB

(ii) PA.PB = PC.PD

`triangleDEF ~ triangleMNK`. If DE = 5 and MN = 6, then find the value of `(A(triangleDEF))/(A(triangleMNK))`

Draw `angle ABC` of measure 80° and bisect it

In the following figure, seg DH ⊥ seg EF and seg GK ⊥ seg EF. If DH = 18 cm, GK = 30 cm and `A(triangle DEF) = 450 cm^2`, then find:

1) EF

2) `A(triangle GFE)`

3) `A(square DFGE)`

On which axis do the following points lie?

R(−4,0)

In the following figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and \[\text{AD} = 9 \text{ find} \frac{A\left( \Delta ABE \right)}{A\left( \Delta BAD \right)} \cdot\]

Draw ∠ABC of measures 135^°and bisect it.

In the given figure, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF. 

Proof :  In ΔXDE, PQ || DE         ...`square`

∴ `"XP"/square = square/"QE"`                               ...(I) (Basic proportionality theorem)

In ΔXEF, QR || EF                       ...`square`

∴ `square/square = square/square                                                           ..."(II)" square`

∴ `square/square = square/square`                                ...from (I) and (II)

∴ seg PR || seg DF           ...(converse of basic proportionality theorem)

In ∆ABC, ray BD bisects ∠ABC and ray CE bisects ∠ACB. If seg AB ≅ seg AC then prove that ED || BC. 

In the given figure, ∠ABC = 75°, ∠EDC = 75° state which two triangles are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.

Are the triangles in the given figure similar? If yes, by which test? 

As shown in figure, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time?