Advertisements
Advertisements
प्रश्न
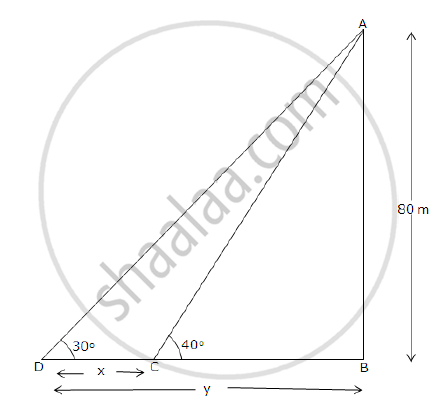
As observed from the top of an 80 m tall lighthouse, the angles of depression of two ships on the same side of the lighthouse of the horizontal line with its base are 30° and 40° respectively. Find the distance between the two ships. Give your answer correct to the nearest meter.
उत्तर
Let AB be the lighthouse and C and D be the two ships.
The angles of depression of the 2 ships are 30° and 40°
So, ∠ADB = 30°
∠ACB = 40°
Let the distance between the ships be CD = x m.
Also, Let BD = y m.
In ΔABC
`tan 40^@ = 80/(y - x)`
`=> y - x = 80/0.8390 = 95.352` ....(1)
Also from ΔABD
`tan 30^@ = 80/y`
`=> y = 80sqrt3 = 80 xx 1.732m` = 138.56 m
From (1) we get
`138.56 - x = 95.352`
`=> x = 138.56 - 95.352 cm = 43.208 m ~~ 43m`
APPEARS IN
संबंधित प्रश्न
Prove the following identities, where the angles involved are acute angles for which the expressions are defined:
`(sin theta-2sin^3theta)/(2cos^3theta -costheta) = tan theta`
Prove that `(sec theta - 1)/(sec theta + 1) = ((sin theta)/(1 + cos theta))^2`
Prove the following identities:
`(1 + cosA)/(1 - cosA) = tan^2A/(secA - 1)^2`
What is the value of \[\frac{\tan^2 \theta - \sec^2 \theta}{\cot^2 \theta - {cosec}^2 \theta}\]
Prove the following identity :
`cos^4A - sin^4A = 2cos^2A - 1`
Prove the following identity :
`[1/((sec^2θ - cos^2θ)) + 1/((cosec^2θ - sin^2θ))](sin^2θcos^2θ) = (1 - sin^2θcos^2θ)/(2 + sin^2θcos^2θ)`
Prove that `sinA/sin(90^circ - A) + cosA/cos(90^circ - A) = sec(90^circ - A) cosec(90^circ - A)`
Without using the trigonometric table, prove that
cos 1°cos 2°cos 3° ....cos 180° = 0.
Prove that identity:
`(sec A - 1)/(sec A + 1) = (1 - cos A)/(1 + cos A)`
If cos (α + β) = 0, then sin (α – β) can be reduced to ______.
