Advertisements
Advertisements
प्रश्न
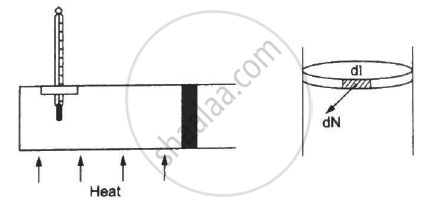
Figure shows a cylindrical tube of radius 5 cm and length 20 cm. It is closed by a tight-fitting cork. The friction coefficient between the cork and the tube is 0.20. The tube contains an ideal gas at a pressure of 1 atm and a temperature of 300 K. The tube is slowly heated and it is found that the cork pops out when the temperature reaches 600 K. Let dN denote the magnitude of the normal contact force exerted by a small length dlof the cork along the periphery (see the figure). Assuming that the temperature of the gas is uniform at any instant, calculate `(dN)/(dt)`.
उत्तर
Here ,
`P_1 = 10^5 "Pa"`
`A = π(0.05)^2`
L = 0.2 m
`V = AL = 0.0016 \text ( m)^3`
`T_1 = 300 K`
`T_2 = 600 K `
`µ = 0.20`
Applying 5 variable equation of state , we get
`(P_1V)/T_1 = (P_2V)/T_2`
⇒ `P_1/T_1 = P_2/T_2`
⇒ `P_2 = T_2/T_1 × P_1 = 600/300 × 10^5`
⇒ `P_2 = 2 × 10^5`
Net pressure , `P = P_2 - P_1 = 2 × 10^5 - 10^5 = 10^5`
Total force acting on the stopper = `PA = 10^5×pi×(0.05)^2`
Applying law of friction , we get
`F = µN = 0.2N`
⇒ `N = F/µ = (10^5×pi×(0.05)^2)/0.2`
`(dN)/(dl) = N/(2pir) = (10^5×pi×(0.05)^2)/(0.2×2pi×(0.05))=0.125×10^5`
⇒ `(dN)/(dl) = 1.25×10^4 N/m`
APPEARS IN
संबंधित प्रश्न
When you come out of a river after a dip, you feel cold. Explain.
Find the number of molecules of an ideal gas in a volume of 1.000 cm3 at STP.
A gas cylinder has walls that can bear a maximum pressure of 1.0 × 106 Pa. It contains a gas at 8.0 × 105 Pa and 300 K. The cylinder is steadily heated. Neglecting any change in the volume, calculate the temperature at which the cylinder will break.
The average translational kinetic energy of air molecules is 0.040 eV (1 eV = 1.6 × 10−19J). Calculate the temperature of the air. Boltzmann constant k = 1.38 × 10−23 J K−1.
An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60°? Assume the temperature to remain constant.
Answer in brief:
What will happen to the mean square speed of the molecules of a gas if the temperature of the gas increases?
At what temperature will oxygen molecules have same rms speed as helium molecules at S.T.P.? (Molecular masses of oxygen and helium are 32 and 4 respectively).
If the density of oxygen is 1.44 kg/m3 at a pressure of 105 N/m2, find the root mean square velocity of oxygen molecules.
Find the kinetic energy of 5 litres of a gas at STP, given the standard pressure is 1.013 × 105 N/m2.
Calculate the average molecular kinetic energy
- per kmol
- per kg
- per molecule
of oxygen at 127°C, given that the molecular weight of oxygen is 32, R is 8.31 J mol−1K−1 and Avogadro’s number NA is 6.02 × 1023 molecules mol−1.
The emissive power of a sphere of area 0.02 m2 is 0.5 kcal s-1m-2. What is the amount of heat radiated by the spherical surface in 20 seconds?
Find the temperature of a blackbody if its spectrum has a peak at (a) λmax = 700 nm (visible), (b) λmax = 3 cm (microwave region) (c) λmax = 3 m (short radio waves). (Take Wien’s constant b = 2.897 × 10-3 m.K).
Calculate the energy radiated in one minute by a blackbody of surface area 200 cm2 at 127 °C (σ = 5.7 x 10-8 J m-2 s-1 K-4)
A metal cube of length 4 cm radiates heat at the rate of 10 J/s. Find its emissive power at a given temperature.
A cylinder containing an ideal gas is in vertical position and has a piston of mass M that is able to move up or down without friction (Figure). If the temperature is increased ______.
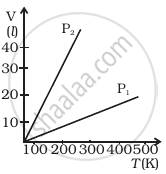
Volume versus temperature graphs for a given mass of an ideal gas are shown in figure at two different values of constant pressure. What can be inferred about relation between P1 and P2?
A gas mixture consists of molecules of types A, B and C with masses mA > mB > mC. Rank the three types of molecules in decreasing order of rms speeds.
Explain why there is no atmosphere on moon.
For a particle moving in vertical circle, the total energy at different positions along the path ______.
