Advertisements
Advertisements
प्रश्न
Find the distance of the line 4x + 7y + 5 = 0 from the point (1, 2) along the line 2x – y = 0.
उत्तर
Let the equation of line PC be 2x – y = 0 on which point P(1, 2) lies.
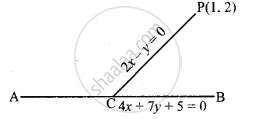
On solving the equation of line AB 4x + 7y + 5 = 0 and 2x – y = 0,
∴ x = `(-5)/18`
and y = `-5/9`
∴ The coordinates of C are `((-5)/18, (-5)/9)` which is the intersection point and the coordinates of P are (1, 2).
Required length PC = `sqrt((-5/18 - 1)^2 + ((-5)/9 - 2)^2)`
= `sqrt(((-23)/18)^2 + ((-23)/9)^2)`
= `23/9 sqrt((1/2)^2 + 1)`
= `23/9 xx sqrt5/2`
= `(23sqrt5)/18`
APPEARS IN
संबंधित प्रश्न
If the lines `(x-1)/2=(y+1)/3=(z-1)/4 ` and `(x-3)/1=(y-k)/2=z/1` intersect each other then find value of k
Find the distance between parallel lines l (x + y) + p = 0 and l (x + y) – r = 0
If sum of the perpendicular distances of a variable point P (x, y) from the lines x + y – 5 = 0 and 3x – 2y+ 7 = 0 is always 10. Show that P must move on a line.
Find the co-ordinates of the point, which divides the line segment joining the points A(2, − 6, 8) and B(− 1, 3, − 4) externally in the ratio 1 : 3.
Find the equation of the line whose perpendicular distance from the origin is 4 units and the angle which the normal makes with the positive direction of x-axis is 15°.
Find the equation of the straight line at a distance of 3 units from the origin such that the perpendicular from the origin to the line makes an angle tan−1 \[\left( \frac{5}{12} \right)\] with the positive direction of x-axi .
A line a drawn through A (4, −1) parallel to the line 3x − 4y + 1 = 0. Find the coordinates of the two points on this line which are at a distance of 5 units from A.
Find the distance of the point (3, 5) from the line 2x + 3y = 14 measured parallel to the line x − 2y = 1.
Find the distance of the line 2x + y = 3 from the point (−1, −3) in the direction of the line whose slope is 1.
Find the equation of a line perpendicular to the line \[\sqrt{3}x - y + 5 = 0\] and at a distance of 3 units from the origin.
Find the distance of the point (4, 5) from the straight line 3x − 5y + 7 = 0.
Find the perpendicular distance of the line joining the points (cos θ, sin θ) and (cos ϕ, sin ϕ) from the origin.
Show that the perpendiculars let fall from any point on the straight line 2x + 11y − 5 = 0 upon the two straight lines 24x + 7y = 20 and 4x − 3y − 2 = 0 are equal to each other.
Find the distance of the point of intersection of the lines 2x + 3y = 21 and 3x − 4y + 11 = 0 from the line 8x + 6y + 5 = 0.
Find the perpendicular distance from the origin of the perpendicular from the point (1, 2) upon the straight line \[x - \sqrt{3}y + 4 = 0 .\]
What are the points on y-axis whose distance from the line \[\frac{x}{3} + \frac{y}{4} = 1\] is 4 units?
Find the equations of the lines through the point of intersection of the lines x − y + 1 = 0 and 2x − 3y+ 5 = 0, whose distance from the point(3, 2) is 7/5.
Write the distance between the lines 4x + 3y − 11 = 0 and 8x + 6y − 15 = 0.
Write the locus of a point the sum of whose distances from the coordinates axes is unity.
L is a variable line such that the algebraic sum of the distances of the points (1, 1), (2, 0) and (0, 2) from the line is equal to zero. The line L will always pass through
The distance between the orthocentre and circumcentre of the triangle with vertices (1, 2), (2, 1) and \[\left( \frac{3 + \sqrt{3}}{2}, \frac{3 + \sqrt{3}}{2} \right)\] is
The line segment joining the points (−3, −4) and (1, −2) is divided by y-axis in the ratio
Distance between the lines 5x + 3y − 7 = 0 and 15x + 9y + 14 = 0 is
The ratio in which the line 3x + 4y + 2 = 0 divides the distance between the line 3x + 4y + 5 = 0 and 3x + 4y − 5 = 0 is
Find the distance between the lines 3x + 4y = 9 and 6x + 8y = 15.
Show that the locus of the mid-point of the distance between the axes of the variable line x cosα + y sinα = p is `1/x^2 + 1/y^2 = 4/p^2` where p is a constant.
Find the points on the line x + y = 4 which lie at a unit distance from the line 4x + 3y = 10.
The distance of the point of intersection of the lines 2x – 3y + 5 = 0 and 3x + 4y = 0 from the line 5x – 2y = 0 is ______.
A point moves so that square of its distance from the point (3, –2) is numerically equal to its distance from the line 5x – 12y = 3. The equation of its locus is ______.
The value of the λ, if the lines (2x + 3y + 4) + λ (6x – y + 12) = 0 are
| Column C1 | Column C2 |
| (a) Parallel to y-axis is | (i) λ = `-3/4` |
| (b) Perpendicular to 7x + y – 4 = 0 is | (ii) λ = `-1/3` |
| (c) Passes through (1, 2) is | (iii) λ = `-17/41` |
| (d) Parallel to x axis is | λ = 3 |
Find the length of the perpendicular drawn from the point P(3, 2, 1) to the line `overliner = (7hati + 7hatj + 6hatk) + λ(-2hati + 2hatj + 3hatk)`
