Advertisements
Advertisements
प्रश्न
If l, m, n are the direction cosines of a line, then prove that l2 + m2 + n2 = 1. Hence find the
direction angle of the line with the X axis which makes direction angles of 135° and 45° with Y and Z axes respectively.
उत्तर
Let `alpha,beta,gamma ` be the angles made by the line with X-, Y-, Z- axes respectively.
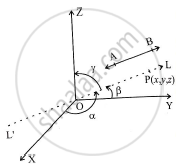
`l=cosalpha, m=cosbeta and n=cosgamma`
Let `bara=a_1hati+a_2hatj+a_3hatk` be any non-zero vector along the line.
Since `hati` is the unit vector along X-axis,
`bara.hati=|bara|.|hati|cosalpha=acosalpha`
Also, `bara.hati=(a_1hati+a_2hatj+a_3hatk).hati`
`=a_1xx1+a_2xx0+a_3xx0=a_1`
`acosalpha=a_1` ..............................(1)
Since `hatj` is the unit vector along Y-axis,
`bara.hatj=|bara|.|hatj|cosbeta=acosbeta`
`bara.hatj=(a_1hati+a_2hatj+a_3hatk).hatj`
`=a_1xx0+a_2xx1+a_3xx0=a_2`
`acosbeta=a_2` ......................(2)
similarly `acosgamma=a_3` .............(3)
from equations (1), (2) and (3),
`a^2cos^2alpha+a^2cos^2beta+a^2cos^2gamma=a_1^2+a_2^2+a_3^2`
`a^2(cos^2alpha+cos^2beta+cos^2gamma)=a^2 ` `[a=|bara|=sqrt(a_1^2+a_2^2+a_3^2)]`
`therefore cos^2alpha+cos^2beta+cos^2gamma=1`
`i.e l^2+m^2+n^2=1`
also
`alpha=?, beta=135^@,gamma=45^@`
`cos^2alpha+cos^2beta+cos^2gamma=45^@`
`cos^2alpha+cos^2 135^@+cos^2 45^@=1`
`cos^2alpha+1/2+1/2=1`
`cos^alpha=0`
`therefore alpha=pi/2 or (3pi)/2`
APPEARS IN
संबंधित प्रश्न
Find the direction cosines of the line
`(x+2)/2=(2y-5)/3; z=-1`
If the lines `(x-1)/(-3) = (y -2)/(2k) = (z-3)/2 and (x-1)/(3k) = (y-1)/1 = (z -6)/(-5)` are perpendicular, find the value of k.
Find the vector equation of the plane passing through (1, 2, 3) and perpendicular to the plane `vecr.(hati + 2hatj -5hatk) + 9 = 0`
Find the direction cosines of the line passing through two points (−2, 4, −5) and (1, 2, 3) .
Using direction ratios show that the points A (2, 3, −4), B (1, −2, 3) and C (3, 8, −11) are collinear.
Find the direction cosines of the sides of the triangle whose vertices are (3, 5, −4), (−1, 1, 2) and (−5, −5, −2).
Find the angle between the vectors whose direction cosines are proportional to 2, 3, −6 and 3, −4, 5.
Find the acute angle between the lines whose direction ratios are proportional to 2 : 3 : 6 and 1 : 2 : 2.
Show that the line through the points (1, −1, 2) and (3, 4, −2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Find the angle between the lines whose direction cosines are given by the equations
(i) l + m + n = 0 and l2 + m2 − n2 = 0
Find the angle between the lines whose direction cosines are given by the equations
2l − m + 2n = 0 and mn + nl + lm = 0
Find the angle between the lines whose direction cosines are given by the equations
l + 2m + 3n = 0 and 3lm − 4ln + mn = 0
Define direction cosines of a directed line.
What are the direction cosines of X-axis?
Write the distance of the point (3, −5, 12) from X-axis?
Write the ratio in which YZ-plane divides the segment joining P (−2, 5, 9) and Q (3, −2, 4).
If a line has direction ratios proportional to 2, −1, −2, then what are its direction consines?
If a unit vector `vec a` makes an angle \[\frac{\pi}{3} \text{ with } \hat{i} , \frac{\pi}{4} \text{ with } \hat{j}\] and an acute angle θ with \[\hat{ k} \] ,then find the value of θ.
Ratio in which the xy-plane divides the join of (1, 2, 3) and (4, 2, 1) is
If P (3, 2, −4), Q (5, 4, −6) and R (9, 8, −10) are collinear, then R divides PQ in the ratio
Verify whether the following ratios are direction cosines of some vector or not
`1/sqrt(2), 1/2, 1/2`
Verify whether the following ratios are direction cosines of some vector or not
`4/3, 0, 3/4`
Find the direction cosines and direction ratios for the following vector
`hat"j"`
Find the direction cosines and direction ratios for the following vector
`hat"i" - hat"k"`
A triangle is formed by joining the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). Find the direction cosines of the medians
If `vec"a" = 2hat"i" + 3hat"j" - 4hat"k", vec"b" = 3hat"i" - 4hat"j" - 5hat"k"`, and `vec"c" = -3hat"i" + 2hat"j" + 3hat"k"`, find the magnitude and direction cosines of `vec"a", vec"b", vec"c"`
If `vec"a" = 2hat"i" + 3hat"j" - 4hat"k", vec"b" = 3hat"i" - 4hat"j" - 5hat"k"`, and `vec"c" = -3hat"i" + 2hat"j" + 3hat"k"`, find the magnitude and direction cosines of `3vec"a"- 2vec"b"+ 5vec"c"`
Choose the correct alternative:
The unit vector parallel to the resultant of the vectors `hat"i" + hat"j" - hat"k"` and `hat"i" - 2hat"j" + hat"k"` is
P is a point on the line segment joining the points (3, 2, –1) and (6, 2, –2). If x co-ordinate of P is 5, then its y co-ordinate is ______.
If α, β, γ are the angles that a line makes with the positive direction of x, y, z axis, respectively, then the direction cosines of the line are ______.
O is the origin and A is (a, b, c). Find the direction cosines of the line OA and the equation of plane through A at right angle to OA.
The area of the quadrilateral ABCD, where A(0,4,1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2), is equal to ______.
A line in the 3-dimensional space makes an angle θ `(0 < θ ≤ π/2)` with both the x and y axes. Then the set of all values of θ is the interval ______.
If the equation of a line is x = ay + b, z = cy + d, then find the direction ratios of the line and a point on the line.
Find the coordinates of the foot of the perpendicular drawn from point (5, 7, 3) to the line `(x - 15)/3 = (y - 29)/8 = (z - 5)/-5`.
Find the coordinates of the image of the point (1, 6, 3) with respect to the line `vecr = (hatj + 2hatk) + λ(hati + 2hatj + 3hatk)`; where 'λ' is a scalar. Also, find the distance of the image from the y – axis.
If a line makes an angle α, β and γ with positive direction of the coordinate axes, then the value of sin2α + sin2β + sin2γ will be ______.
