Advertisements
Advertisements
प्रश्न
If l, m, n are the direction cosines of a line, then prove that l2 + m2 + n2 = 1. Hence find the
direction angle of the line with the X axis which makes direction angles of 135° and 45° with Y and Z axes respectively.
उत्तर
Let `alpha,beta,gamma ` be the angles made by the line with X-, Y-, Z- axes respectively.
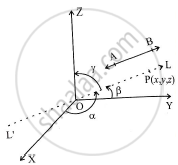
`l=cosalpha, m=cosbeta and n=cosgamma`
Let `bara=a_1hati+a_2hatj+a_3hatk` be any non-zero vector along the line.
Since `hati` is the unit vector along X-axis,
`bara.hati=|bara|.|hati|cosalpha=acosalpha`
Also, `bara.hati=(a_1hati+a_2hatj+a_3hatk).hati`
`=a_1xx1+a_2xx0+a_3xx0=a_1`
`acosalpha=a_1` ..............................(1)
Since `hatj` is the unit vector along Y-axis,
`bara.hatj=|bara|.|hatj|cosbeta=acosbeta`
`bara.hatj=(a_1hati+a_2hatj+a_3hatk).hatj`
`=a_1xx0+a_2xx1+a_3xx0=a_2`
`acosbeta=a_2` ......................(2)
similarly `acosgamma=a_3` .............(3)
from equations (1), (2) and (3),
`a^2cos^2alpha+a^2cos^2beta+a^2cos^2gamma=a_1^2+a_2^2+a_3^2`
`a^2(cos^2alpha+cos^2beta+cos^2gamma)=a^2 ` `[a=|bara|=sqrt(a_1^2+a_2^2+a_3^2)]`
`therefore cos^2alpha+cos^2beta+cos^2gamma=1`
`i.e l^2+m^2+n^2=1`
also
`alpha=?, beta=135^@,gamma=45^@`
`cos^2alpha+cos^2beta+cos^2gamma=45^@`
`cos^2alpha+cos^2 135^@+cos^2 45^@=1`
`cos^2alpha+1/2+1/2=1`
`cos^alpha=0`
`therefore alpha=pi/2 or (3pi)/2`
APPEARS IN
संबंधित प्रश्न
Direction cosines of the line passing through the points A (- 4, 2, 3) and B (1, 3, -2) are.........
Write the direction ratios of the following line :
`x = −3, (y−4)/3 =( 2 −z)/1`
Find the direction cosines of a line which makes equal angles with the coordinate axes.
If a line has the direction ratios −18, 12, −4, then what are its direction cosines?
Find the vector equation of the plane passing through (1, 2, 3) and perpendicular to the plane `vecr.(hati + 2hatj -5hatk) + 9 = 0`
Find the angle between the vectors with direction ratios proportional to 1, −2, 1 and 4, 3, 2.
Find the angle between the vectors whose direction cosines are proportional to 2, 3, −6 and 3, −4, 5.
Find the direction cosines of the lines, connected by the relations: l + m +n = 0 and 2lm + 2ln − mn= 0.
Find the angle between the lines whose direction cosines are given by the equations
(i) l + m + n = 0 and l2 + m2 − n2 = 0
Find the angle between the lines whose direction cosines are given by the equations
2l + 2m − n = 0, mn + ln + lm = 0
What are the direction cosines of Z-axis?
Write the angle between the lines whose direction ratios are proportional to 1, −2, 1 and 4, 3, 2.
Write the distance of the point P (x, y, z) from XOY plane.
Write the coordinates of the projection of the point P (2, −3, 5) on Y-axis.
If a line has direction ratios proportional to 2, −1, −2, then what are its direction consines?
If a line makes angles 90° and 60° respectively with the positive directions of x and y axes, find the angle which it makes with the positive direction of z-axis.
For every point P (x, y, z) on the xy-plane,
If the x-coordinate of a point P on the join of Q (2, 2, 1) and R (5, 1, −2) is 4, then its z-coordinate is
The angle between the two diagonals of a cube is
Find the direction cosines of the line joining the points P(4,3,-5) and Q(-2,1,-8) .
Find the vector equation of a line passing through the point (2, 3, 2) and parallel to the line `vec("r") = (-2hat"i"+3hat"j") +lambda(2hat"i"-3hat"j"+6hat"k").`Also, find the distance between these two lines.
Verify whether the following ratios are direction cosines of some vector or not
`1/sqrt(2), 1/2, 1/2`
Find the direction cosines and direction ratios for the following vector
`3hat"i" - 4hat"j" + 8hat"k"`
Find the direction cosines and direction ratios for the following vector
`3hat"i" + hat"j" + hat"k"`
Find the direction cosines and direction ratios for the following vector
`3hat"i" - 3hat"k" + 4hat"j"`
Find the direction cosines and direction ratios for the following vector
`hat"i" - hat"k"`
If (a, a + b, a + b + c) is one set of direction ratios of the line joining (1, 0, 0) and (0, 1, 0), then find a set of values of a, b, c
Find the direction cosines of the line passing through the points P(2, 3, 5) and Q(–1, 2, 4).
P is a point on the line segment joining the points (3, 2, –1) and (6, 2, –2). If x co-ordinate of P is 5, then its y co-ordinate is ______.
The area of the quadrilateral ABCD, where A(0,4,1), B(2, 3, –1), C(4, 5, 0) and D(2, 6, 2), is equal to ______.
Find the direction cosine of a line which makes equal angle with coordinate axes.
What will be the value of 'P' so that the lines `(1 - x)/3 = (7y - 14)/(2P) = (z - 3)/2` and `(7 - 7x)/(3P) = (y - 5)/1 = (6 - z)/5` at right angles.
The d.c's of a line whose direction ratios are 2, 3, –6, are ______.
If the equation of a line is x = ay + b, z = cy + d, then find the direction ratios of the line and a point on the line.
