Advertisements
Advertisements
प्रश्न
The angle between the two diagonals of a cube is
पर्याय
(a) 30°
(b) 45°
(c) \[\cos^{- 1} \left( \frac{1}{\sqrt{3}} \right)\]
(d) \[\cos^{- 1} \left( \frac{1}{3} \right)\]
Advertisements
उत्तर
\[\cos^{- 1} \left( \frac{1}{3} \right)\]
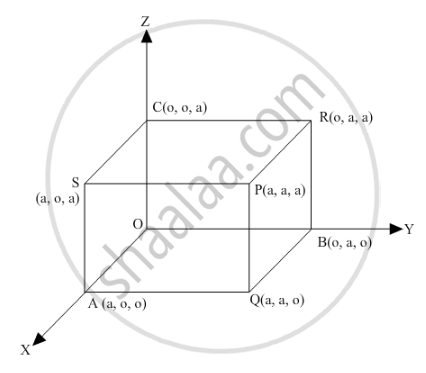
\[\text { Let a be the length of an edge of the cube and let one corner be at the origin as shown in the figure . Clearly, OP, AR, BS, and CQ are the diagonals of the cube } . \]
\[\text{ Consider the diagonals OP and AR } . \]
\[\text{ Direction ratios of OP and AR are proportional to a - 0, a - 0, a - 0 and 0 - a, a - 0, a - 0, i . e . a, a, a and - a, a, a, respectively } . \]
\[\text { Let } \theta \text{ be the angle between OP and AR . Then,} \]
\[\cos \theta = \frac{a \times - a + a \times a + a \times a}{\sqrt{a^2 + a^2 + a^2}\sqrt{\left( - a \right)^2 + a^2 + a^2}}\]
\[ \Rightarrow \cos \theta = \frac{- a^2 + a^2 + a^2}{\sqrt{3 a^2}\sqrt{3 a^2}}\]
\[ \Rightarrow \cos \theta = \frac{1}{3} \]
\[ \Rightarrow \theta = \cos^{- 1} \left( \frac{1}{3} \right) \]
\[\text{ Similarly, the angles between other pairs of the diagonals are equal to } \cos^{- 1} \left( \frac{1}{3} \right) \text{ as the angle between any two diagonals of a cube is } \cos^{- 1} \left( \frac{1}{3} \right) .\]
APPEARS IN
संबंधित प्रश्न
Which of the following represents direction cosines of the line :
(a)`0,1/sqrt2,1/2`
(b)`0,-sqrt3/2,1/sqrt2`
(c)`0,sqrt3/2,1/2`
(d)`1/2,1/2,1/2`
Find the vector equation of the plane passing through (1, 2, 3) and perpendicular to the plane `vecr.(hati + 2hatj -5hatk) + 9 = 0`
Find the direction cosines of the line passing through two points (−2, 4, −5) and (1, 2, 3) .
Find the angle between the vectors with direction ratios proportional to 1, −2, 1 and 4, 3, 2.
Find the angle between the vectors whose direction cosines are proportional to 2, 3, −6 and 3, −4, 5.
Find the acute angle between the lines whose direction ratios are proportional to 2 : 3 : 6 and 1 : 2 : 2.
Find the angle between the lines whose direction cosines are given by the equations
2l − m + 2n = 0 and mn + nl + lm = 0
What are the direction cosines of Y-axis?
Write the distances of the point (7, −2, 3) from XY, YZ and XZ-planes.
Write the ratio in which YZ-plane divides the segment joining P (−2, 5, 9) and Q (3, −2, 4).
A line makes an angle of 60° with each of X-axis and Y-axis. Find the acute angle made by the line with Z-axis.
Write the angle between the lines whose direction ratios are proportional to 1, −2, 1 and 4, 3, 2.
If a line has direction ratios proportional to 2, −1, −2, then what are its direction consines?
If a unit vector `vec a` makes an angle \[\frac{\pi}{3} \text{ with } \hat{i} , \frac{\pi}{4} \text{ with } \hat{j}\] and an acute angle θ with \[\hat{ k} \] ,then find the value of θ.
If a line makes angles 90° and 60° respectively with the positive directions of x and y axes, find the angle which it makes with the positive direction of z-axis.
A parallelopiped is formed by planes drawn through the points (2, 3, 5) and (5, 9, 7), parallel to the coordinate planes. The length of a diagonal of the parallelopiped is
If O is the origin, OP = 3 with direction ratios proportional to −1, 2, −2 then the coordinates of P are
Find the direction cosines of a vector whose direction ratios are
0, 0, 7
Find the direction cosines and direction ratios for the following vector
`3hat"i" - 3hat"k" + 4hat"j"`
If a line makes an angle of 30°, 60°, 90° with the positive direction of x, y, z-axes, respectively, then find its direction cosines.
If α, β, γ are the angles that a line makes with the positive direction of x, y, z axis, respectively, then the direction cosines of the line are ______.
If a line makes angles `pi/2, 3/4 pi` and `pi/4` with x, y, z axis, respectively, then its direction cosines are ______.
If a variable line in two adjacent positions has direction cosines l, m, n and l + δl, m + δm, n + δn, show that the small angle δθ between the two positions is given by δθ2 = δl2 + δm2 + δn2
If the directions cosines of a line are k,k,k, then ______.
If a line makes angles 90°, 135°, 45° with x, y and z-axis respectively then which of the following will be its direction cosine.
Find the direction cosine of a line which makes equal angle with coordinate axes.
If a line has the direction ratio – 18, 12, – 4, then what are its direction cosine.
What will be the value of 'P' so that the lines `(1 - x)/3 = (7y - 14)/(2P) = (z - 3)/2` and `(7 - 7x)/(3P) = (y - 5)/1 = (6 - z)/5` at right angles.
If two straight lines whose direction cosines are given by the relations l + m – n = 0, 3l2 + m2 + cnl = 0 are parallel, then the positive value of c is ______.
A line in the 3-dimensional space makes an angle θ `(0 < θ ≤ π/2)` with both the x and y axes. Then the set of all values of θ is the interval ______.
The projections of a vector on the three coordinate axis are 6, –3, 2 respectively. The direction cosines of the vector are ______.
Equation of a line passing through point (1, 2, 3) and equally inclined to the coordinate axis, is ______.
If a line makes angles of 90°, 135° and 45° with the x, y and z axes respectively, then its direction cosines are ______.
Find the coordinates of the foot of the perpendicular drawn from point (5, 7, 3) to the line `(x - 15)/3 = (y - 29)/8 = (z - 5)/-5`.
If a line makes an angle α, β and γ with positive direction of the coordinate axes, then the value of sin2α + sin2β + sin2γ will be ______.
