Advertisements
Advertisements
प्रश्न
If x = cot A + cos A and y = cot A – cos A then prove that `((x-y)/(x+y))^2 + ((x-y)/2)^2=1`
उत्तर
LHS = `((x-y)/(x+y))^2 + ((x-y)/2)^2`
=`[((cotA+cosA)-(cotA-cosA))/((cotA+cosA)+(cotA-cosA))]^2 + [((cotA+cosA)-(cotA-cosA))/2]^2`
=`[(cotA+cosA-cotA+cosA)/(cotA+cosA+cotA-cosA)]^2 + [(cotA+cosA-cotA+cosA)/2]^2`
=`[(2cosA)/(2cotA)]^2 + [(2cosA)/2]^2`
=`[(cosA)/(((cosA)/(sinA)))]^2 + [cosA]^2`
=`[(sinA cosA)/cosA]^2 + [cosA]^2`
=`[sinA]^2 + [cosA]^2`
=`sin^2 A + cos^2 A`
=1
=RHS
APPEARS IN
संबंधित प्रश्न
If A, B, C are the interior angles of a ΔABC, show that `cos[(B+C)/2] = sin A/2`
If 3tan θ 4 , show that `((4cos theta - sin theta ))/((4 cos theta + sin theta))=4/5`
If 3 cot `theta = 2, `show that `((4 sin theta - 4 cos theta))/((2 sin theta + 6 cos theta ))=1/3`
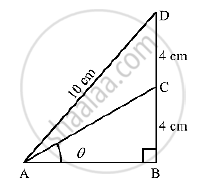
In the adjoining figure, `∠B = 90° , ∠BAC = theta° , BC = CD = 4cm and AD = 10 cm`. find (i) sin theta and (ii) `costheta`
Given: cos A = `( 5 )/ ( 13 )`
Evaluate:
- `(sin "A "–cot "A") / (2 tan "A")`
- `cot "A" + 1/cos"A"`
Given : 5 cos A - 12 sin A = 0; evaluate:
`(sin "A"+cos"A")/(2 cos"A"– sin"A")`
If sin A = cos A, find the value of 2 tan2A - 2 sec2 A + 5.
If cosec A + sin A = 5`(1)/(5)`, find the value of cosec2A + sin2A.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tanB = `(8)/(15)`
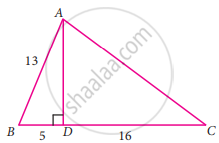
From the given figure, find the values of tan C