Advertisements
Advertisements
प्रश्न
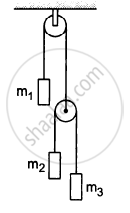
Let m1 = 1 kg, m2 = 2 kg and m3 = 3 kg in the following figure. Find the accelerations of m1, m2 and m3. The string from the upper pulley to m1 is 20 cm when the system is released from rest. How long will it take before m1 strikes the pulley?
उत्तर
The free-body diagram for mass m1 is shown below: a
a
The free-body diagram for mass m2 is shown below: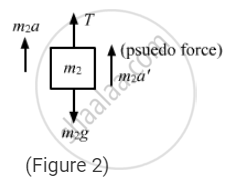
The free-body diagram for mass m3 is shown below: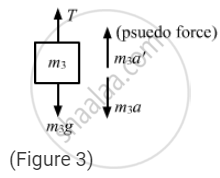
Suppose the block m1 moves upward with acceleration a1 and the blocks m2 and m3have relative acceleration a2 due to the difference of weight between them.
So, the actual acceleration of the blocks m1, m2 and m3 will be a1, (a1 − a2) and (a1 + a2), as shown.
From figure 2, T − 1g − 1a1 = 0 ...(i)
From figure 3,\[\frac{T}{2} - 2g - 2\left( a_1 - a_2 \right) = 0 . . . \left( ii \right)\]
From figure 4,\[\frac{T}{2} - 3g - 3\left( a_1 + a_2 \right) = 0 . . . \left( iii \right)\]
From equations (i) and (ii), eliminating T, we get:
1g + 1a2 = 4g + 4 (a1 + a2)
5a2 − 4a1 = 3g ...(iv)
From equations (ii) and (iii), we get:
2g + 2(a1 − a2) = 3g − 3 (a1 − a2)
5a1 + a2 = g ...(v)
Solving equations (iv) and (v), we get:
\[a_1 = \frac{2g}{29}\]
\[\text{ and }a_2 = g - 5 a_1 \]
\[ \Rightarrow a_2 = g - \frac{10g}{29} = \frac{19g}{29}\]
\[\text{So}, a_1 - a_2 = \frac{2g}{29} - \frac{19g}{29} = - \frac{17g}{29}\]
So, accelerations of m1, m2 and m3 are \[\frac{19g}{29}\left( up \right),
\frac{17g}{29} \left(\text{ down }\right)\text{ and }\frac{21g}{29}\left(\text{ down }\right)\]
Now, u = 0, s = 20 cm = 0.2 m
\[a_2 = \frac{19g}{29} \]
\[ \therefore s = ut + \frac{1}{2}a t^2 \]
\[ \Rightarrow 0 . 2 = \frac{1}{2} \times \frac{19}{29}g t^2 \]
\[ \Rightarrow t = 0 . 25 s\]
APPEARS IN
संबंधित प्रश्न
Two masses 8 kg and 12 kg are connected at the two ends of a light, inextensible string that goes over a frictionless pulley. Find the acceleration of the masses, and the tension in the string when the masses are released.
Explain why a cricketer moves his hands backwards while holding a catch.
A block of mass 0.2 kg is suspended from the ceiling by a light string. A second block of mass 0.3 kg is suspended from the first block by another string. Find the tensions in the two strings. Take g = 10 m/s2.
A particle of mass 0.3 kg is subjected to a force F = −kx with k = 15 N/m. What will be its initial acceleration if it is released from a point x = 20 cm?
An empty plastic box of mass m is found to accelerate up at the rate of g/6 when placed deep inside water. How much sand should be put inside the box so that it may accelerate down at the rate of g/6?
Consider the situation shown in the following figure All the surfaces are frictionless and the string and the pulley are light. Find the magnitude of acceleration of the two blocks.

Find the acceleration of the block of mass M in the situation shown in the following figure. All the surfaces are frictionless and the pulleys and the string are light.
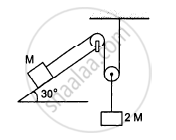
Find the acceleration of the blocks A and B in the three situations shown in the following figure.

A block is kept on the floor of an elevator at rest. The elevator starts descending with an acceleration of 12 m/s2. Find the displacement of the block during the first 0.2 s after the start. Take g = 10 m/s2.
A body of mass m moving with a velocity v is acted upon by a force. Write an expression for change in momentum in each of the following cases: (i) When v << c, (ii) When v → c and (iii) When v << c but m does not remain constant. Here, c is the speed of light.
State Newton's second law of motion. Under what condition does it take the form F = ma?
The correct form of Newton's second law is :
The linear momentum of a body of mass m moving with velocity v is :
Define Newton’s second law of motion.
ame the law of motion which gives the definition of force.
State Newton's second law of motion.
A body of mass 400 g is resting on a frictionless table. Find the acceleration of the body when acted upon by a force of 0.02 N.
Use Newton's second law to explain the following:
We always prefer to land on sand instead of hard floor while taking a high jump.
A ball is thrown upward and reaches a maximum height of 19.6 m. Find its initial speed?
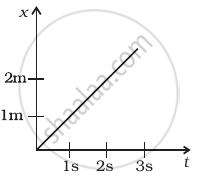
Figure shows (x, t), (y, t ) diagram of a particle moving in 2-dimensions.
|
|
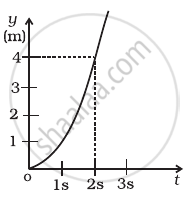 (b) |
If the particle has a mass of 500 g, find the force (direction and magnitude) acting on the particle.