Advertisements
Advertisements
प्रश्न
Prove that
\[2 \tan^{- 1} \left( \frac{1}{5} \right) + \sec^{- 1} \left( \frac{5\sqrt{2}}{7} \right) + 2 \tan^{- 1} \left( \frac{1}{8} \right) = \frac{\pi}{4}\] .
उत्तर
\[2 \tan^{- 1} \left( \frac{1}{5} \right) + se c^{- 1} \left( \frac{5\sqrt{2}}{7} \right) + 2 \tan^{- 1} \left( \frac{1}{8} \right)\]
= \[2 \tan^{- 1} \left( \frac{1}{5} \right) + \tan^{- 1} \left( \sqrt{\left( \frac{5\sqrt{2}}{7} \right)^2 - 1} \right) + 2 \tan^{- 1} \left( \frac{1}{8} \right) \left[ \text { Using }se c^{- 1} x = \tan^{- 1} \sqrt{x^2 - 1} \right]\]
\[= 2 \tan^{- 1} \left( \frac{1}{5} \right) + \tan^{- 1} \left( \frac{1}{7} \right) + 2 \tan^{- 1} \left( \frac{1}{8} \right)\]
= 2 \[\left( \tan^{- 1} \left( \frac{1}{5} \right) + \tan^{- 1} \left( \frac{1}{8} \right) \right) + \tan^{- 1} \left( \frac{1}{7} \right)\]
\[= 2 \tan^{- 1} \left( \frac{\frac{1}{5} + \frac{1}{8}}{1 - \frac{1}{5} \times \frac{1}{8}} \right) + \tan^{- 1} \left( \frac{1}{7} \right) \left[\text { Using} \tan^{- 1} x + \tan^{- 1} y = \tan^{- 1} \left( \frac{x + y}{1 - xy} \right) \right]\]
\[= 2 \tan^{- 1} \left( \frac{13}{39} \right) + \tan^{- 1} \left( \frac{1}{7} \right)\]
\[= 2 \tan^{- 1} \left( \frac{1}{3} \right) + \tan^{- 1} \left( \frac{1}{7} \right)\]
\[= \tan^{- 1} \left( \frac{\frac{2}{3}}{1 - \frac{1}{9}} \right) + \tan^{- 1} \left( \frac{1}{7} \right) \left[ \text { Using} 2 \tan^{- 1} x = \tan^{- 1} \frac{2x}{1 - x^2}, \text { if } \left| x \right| < 1 \right]\]
\[= \tan^{- 1} \left( \frac{3}{4} \right) + \tan^{- 1} \left( \frac{1}{7} \right)\]
\[= \tan^{- 1} \left( \frac{\frac{3}{4} + \frac{1}{7}}{1 - \frac{3}{4} \times \frac{1}{7}} \right)\]
\[= \tan^{- 1} \left( 1 \right)\]
\[ = \frac{\pi}{4}\]
\[ = RHS\]
Hence proved.
APPEARS IN
संबंधित प्रश्न
Prove `2 tan^(-1) 1/2 + tan^(-1) 1/7 = tan^(-1) 31/17`
if `tan^(-1) (x-1)/(x - 2) + tan^(-1) (x + 1)/(x + 2) = pi/4` then find the value of x.
`cos^(-1) (cos (7pi)/6)` is equal to ______.
`sin[pi/3 - sin^(-1) (-1/2)]` is equal to ______.
Solve the following equation:
`2 tan^(-1) (cos x) = tan^(-1) (2 cosec x)`
Solve for x : \[\tan^{- 1} \left( \frac{x - 2}{x - 1} \right) + \tan^{- 1} \left( \frac{x + 2}{x + 1} \right) = \frac{\pi}{4}\] .
Solve for x : \[\cos \left( \tan^{- 1} x \right) = \sin \left( \cot^{- 1} \frac{3}{4} \right)\] .
Solve: tan-1 4 x + tan-1 6x `= π/(4)`.
Prove that `tan^-1 2/11 + tan^-1 7/24 = tan^-1 1/2`
Choose the correct alternative:
If |x| ≤ 1, then `2tan^-1x - sin^-1 (2x)/(1 + x^2)` is equal to
Choose the correct alternative:
If `sin^-1x + cot^-1 (1/2) = pi/2`, then x is equal to
Evaluate tan (tan–1(– 4)).
Evaluate `cos[sin^-1 1/4 + sec^-1 4/3]`
Prove that cot–17 + cot–18 + cot–118 = cot–13
Prove that `sin^-1 8/17 + sin^-1 3/5 = sin^-1 7/85`
If `sin^-1 ((2"a")/(1 + "a"^2)) + cos^-1 ((1 - "a"^2)/(1 + "a"^2)) = tan^-1 ((2x)/(1 - x^2))`. where a, x ∈ ] 0, 1, then the value of x is ______.
The number of real solutions of the equation `sqrt(1 + cos 2x) = sqrt(2) cos^-1 (cos x)` in `[pi/2, pi]` is ______.
The value of cos215° - cos230° + cos245° - cos260° + cos275° is ______.
The maximum value of sinx + cosx is ____________.
If `"sec" theta = "x" + 1/(4 "x"), "x" in "R, x" ne 0,`then the value of `"sec" theta + "tan" theta` is ____________.
The value of `"tan"^-1 (1/2) + "tan"^-1 (1/3) + "tan"^-1 (7/8)` is ____________.
`"tan"^-1 1 + "cos"^-1 ((-1)/2) + "sin"^-1 ((-1)/2)`
If `"cot"^-1 (sqrt"cos" alpha) - "tan"^-1 (sqrt"cos" alpha) = "x",` the sinx is equal to ____________.
`"sin" {2 "cos"^-1 ((-3)/5)}` is equal to ____________.
The value of expression 2 `"sec"^-1 2 + "sin"^-1 (1/2)`
If x = a sec θ, y = b tan θ, then `("d"^2"y")/("dx"^2)` at θ = `π/6` is:
`"cos"^-1["cos"(2"cot"^-1(sqrt2 - 1))]` = ____________.
The Government of India is planning to fix a hoarding board at the face of a building on the road of a busy market for awareness on COVID-19 protocol. Ram, Robert and Rahim are the three engineers who are working on this project. “A” is considered to be a person viewing the hoarding board 20 metres away from the building, standing at the edge of a pathway nearby. Ram, Robert and Rahim suggested to the firm to place the hoarding board at three different locations namely C, D and E. “C” is at the height of 10 metres from the ground level. For viewer A, the angle of elevation of “D” is double the angle of elevation of “C” The angle of elevation of “E” is triple the angle of elevation of “C” for the same viewer. Look at the figure given and based on the above information answer the following:
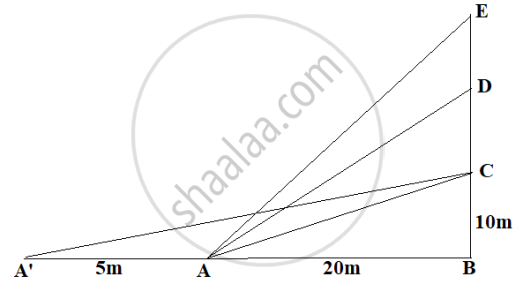
Measure of ∠CAB = ________.
The Simplest form of `cot^-1 (1/sqrt(x^2 - 1))`, |x| > 1 is
Solve:
sin–1(x) + sin–1(1 – x) = cos–1x.
