Advertisements
Advertisements
प्रश्न
Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle α is one-third that of the cone and the greatest volume of cylinder is `4/27 pih^3` tan2α.
उत्तर
Let VAB be a cone.
Height of the cone = h
Semivertex angle = α
Cylinder A'B'DC is inscribed in a cone whose radius = x.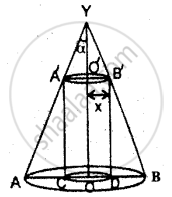
OO' = Height of cylinder = VO - VO'
= h - x cot α
V, volume of the cylinder = πx2 (h - x cot α)
On differentiating with respect to x,
`(dV)/dx = 2 pi xh - 3 pix^2 cot alpha`
For maximum and minimum, `(dV)/dx = 0`
⇒ 2πxh - 3πx2 cot α = 0
⇒ πx (2h - 3x cot α) = 0
⇒ 2h - 3 x cot α = 0
⇒ 3x cot α = 2h
`therefore x = (2h)/3 tan alpha ...[x ne 0]`
Now, `(d^2 v)/(dx^2) = 2 pih - 6 pih cot alpha`
When x = `(2h)/3 tan alpha`
`therefore (d^2V)/dx^2 = 2pih - 6pi (2h)/3 tan alpha cot alpha`
`= 2pih - 4pih`
`= pi(2h - 4h)`
`= - 2 pih < 0`
⇒ V is maximum when x = `(2h)/3 tan alpha`
Height of cylinder, OO' = VO - VO' = h - x cot α
`= h - ((2h)/3 tan alpha) cot alpha ...[because x = (2h)/3 tan alpha]`
`= h - (2h)/3 = h/3`
`= 1/3` height of the cone
Maximum volume of cylinder = πx2 (h - x cot α)
`= pi - ((2h)/3 tan alpha)^2 * (h - (2h)/3)`
`= pi((2h)/3 tan alpha)^2 xx h/3`
`= 4/27 pih^3 tan^2 alpha`
APPEARS IN
संबंधित प्रश्न
f (x) = 2x2 − 5x + 3 on [1, 3] Discuss the applicability of Rolle's theorem for the following function on the indicated intervals ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = x2 − 8x + 12 on [2, 6] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = (x − 1) (x − 2)2 on [1, 2] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = x(x − 1)2 on [0, 1] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = x(x −2)2 on the interval [0, 2] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = cos 2x on [0, π] ?
Verify Rolle's theorem for the following function on the indicated interval f (x) = \[\frac{\sin x}{e^x}\] on 0 ≤ x ≤ π ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = sin 3x on [0, π] ?
Verify Rolle's theorem for the following function on the indicated interval f(x) = 2 sin x + sin 2x on [0, π] ?
Verify Rolle's theorem for the following function on the indicated interval \[f\left( x \right) = \frac{x}{2} - \sin\frac{\pi x}{6} \text { on }[ - 1, 0]\]?
At what point on the following curve, is the tangent parallel to x-axis y = 12 (x + 1) (x − 2) on [−1, 2] ?
Examine if Rolle's theorem is applicable to any one of the following functions.
(i) f (x) = [x] for x ∈ [5, 9]
(ii) f (x) = [x] for x ∈ [−2, 2]
Can you say something about the converse of Rolle's Theorem from these functions?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = x2 − 3x + 2 on [−1, 2] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = 2x2 − 3x + 1 on [1, 3] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem f(x) = 2x − x2 on [0, 1] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem \[f\left( x \right) = x + \frac{1}{x} \text { on }[1, 3]\] ?
Verify Lagrange's mean value theorem for the following function on the indicated intervals. find a point 'c' in the indicated interval as stated by the Lagrange's mean value theorem \[f\left( x \right) = \sqrt{x^2 - 4} \text { on }[2, 4]\] ?
Discuss the applicability of Lagrange's mean value theorem for the function
f(x) = | x | on [−1, 1] ?
Show that the lagrange's mean value theorem is not applicable to the function
f(x) = \[\frac{1}{x}\] on [−1, 1] ?
Find a point on the curve y = x2 + x, where the tangent is parallel to the chord joining (0, 0) and (1, 2) ?
Find the points on the curve y = x3 − 3x, where the tangent to the curve is parallel to the chord joining (1, −2) and (2, 2) ?
For the function f (x) = x + \[\frac{1}{x}\] ∈ [1, 3], the value of c for the Lagrange's mean value theorem is
When the tangent to the curve y = x log x is parallel to the chord joining the points (1, 0) and (e, e), the value of x is
The value of c in Rolle's theorem for the function \[f\left( x \right) = \frac{x\left( x + 1 \right)}{e^x}\] defined on [−1, 0] is
Show that the local maximum value of `x + 1/x` is less than local minimum value.
Find the maximum and minimum values of f(x) = secx + log cos2x, 0 < x < 2π
Find the area of greatest rectangle that can be inscribed in an ellipse `x^2/"a"^2 + y^2/"b"^2` = 1
An isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a. Show that the area of triangle is maximum when θ = `pi/6`
If f(x) = `1/(4x^2 + 2x + 1)`, then its maximum value is ______.
The maximum value of sinx + cosx is ______.
At x = `(5pi)/6`, f(x) = 2 sin3x + 3 cos3x is ______.
If f(x) = ax2 + 6x + 5 attains its maximum value at x = 1, then the value of a is
Let y = `f(x)` be the equation of a curve. Then the equation of tangent at (xo, yo) is :-
