Advertisements
Advertisements
प्रश्न
Statement A (Assertion): For 0 < θ ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Statement R (Reason): cosec2 θ – cot2 θ = 1
विकल्प
Both Assertion (A) and Reason (R) are true; and Reason (R) is the correct explanation of Assertion (A).
Both Assertion (A) and Reason (R) are true; but Reason (R) is not the correct explanation of Assertion (A).
Assertion (A) is true but Reason (R) is false.
Assertion (A) is false but Reason (R) is true.
उत्तर
Both Assertion (A) and Reason (R) are true; and Reason (R) is the correct explanation of Assertion (A).
Explanation:
∵ cosec2 θ – cot2 θ = 1
`\implies` (cosec θ – cot θ) (cosec θ + cot θ) = 1
`\implies` (cosec θ – cot θ) = `1/("cosec" θ + cot θ)`
∴ It is clear that cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
APPEARS IN
संबंधित प्रश्न
If sin θ ,` sqrt (3)/2` find the value of all T- ratios of θ .
If sec `theta = 17/8 ` verify that `((3-4sin^2theta)/(4 cos^2theta -3))=((3-tan^2theta)/(1-tan^2theta))`
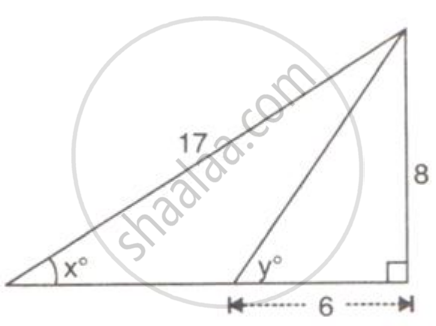
Use the given figure to find :
(i) sin xo
(ii) cos yo
(iii) 3 tan xo - 2 sin yo + 4 cos yo.
In the figure given below, ABC is an isosceles triangle with BC = 8 cm and AB = AC = 5 cm. Find:
(i) sin B
(ii) tan C
(iii) sin2 B + cos2B
(iv) tan C - cot B
Given : 5 cos A - 12 sin A = 0; evaluate:
`(sin "A"+cos"A")/(2 cos"A"– sin"A")`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cose C = `(15)/(11)`
In an isosceles triangle ABC, AB = BC = 6 cm and ∠B = 90°. Find the values of cos C
If sin A = `(7)/(25)`, find the value of : cot2A - cosec2A
From the given figure, find all the trigonometric ratios of angle B
If cos A = `3/5`, then find the value of `(sin"A" - cos"A")/(2tan"A")`
