Advertisements
Advertisements
प्रश्न
The equation of the straight line which passes through the point (−4, 3) such that the portion of the line between the axes is divided internally by the point in the ratio 5 : 3 is
विकल्प
9x − 20y + 96 = 0
9x + 20y = 24
20x + 9y + 53 = 0
none of these
Advertisements
उत्तर
9x − 20y + 96 = 0
Let the required line intersects the coordinate axis at (a, 0) and (0, b).
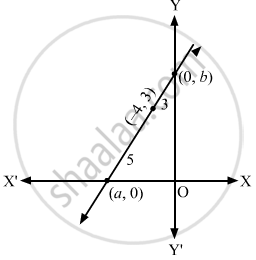
The point (−4, 3) divides the required line in the ratio 5 : 3
\[\therefore - 4 = \frac{5 \times 0 + 3 \times a}{5 + 3} \text { and } 3 = \frac{5 \times b + 3 \times 0}{5 + 3}\]
\[ \Rightarrow a = \frac{- 32}{3} \text { and } b = \frac{24}{5}\]
Hence, The equation of the required line is given below:
\[\frac{x}{\frac{- 32}{3}} + \frac{y}{\frac{24}{5}} = 1\]
\[ \Rightarrow \frac{- 3x}{32} + \frac{5y}{24} = 1\]
\[ \Rightarrow - 9x + 20y = 96\]
\[ \Rightarrow 9x - 20y + 96 = 0\]
APPEARS IN
संबंधित प्रश्न
Find the equation of the straight line passing through the point (6, 2) and having slope − 3.
Find the equation of the straight line passing through (3, −2) and making an angle of 60° with the positive direction of y-axis.
Find the equation of the line passing through the point (−3, 5) and perpendicular to the line joining (2, 5) and (−3, 6).
Find the equation of the straight lines passing through the following pair of point :
(0, 0) and (2, −2)
Find the equation of the straight lines passing through the following pair of point:
(a, b) and (a + c sin α, b + c cos α)
Find the equation of the straight lines passing through the following pair of point :
(at1, a/t1) and (at2, a/t2)
Find the equation to the straight line cutting off intercepts 3 and 2 from the axes.
Find the equation of the line which passes through the point (− 4, 3) and the portion of the line intercepted between the axes is divided internally in the ratio 5 : 3 by this point.
A straight line passes through the point (α, β) and this point bisects the portion of the line intercepted between the axes. Show that the equation of the straight line is \[\frac{x}{2 \alpha} + \frac{y}{2 \beta} = 1\].
Find the equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.
Find the equation of the straight line which passes through the point P (2, 6) and cuts the coordinate axes at the point A and B respectively so that \[\frac{AP}{BP} = \frac{2}{3}\] .
Find the equations of the straight lines each of which passes through the point (3, 2) and cuts off intercepts a and b respectively on X and Y-axes such that a − b = 2.
Find the equation of the straight line passing through the point (2, 1) and bisecting the portion of the straight line 3x − 5y = 15 lying between the axes.
A straight line drawn through the point A (2, 1) making an angle π/4 with positive x-axis intersects another line x + 2y + 1 = 0 in the point B. Find length AB.
If the straight line \[\frac{x}{a} + \frac{y}{b} = 1\] passes through the point of intersection of the lines x + y = 3 and 2x − 3y = 1 and is parallel to x − y − 6 = 0, find a and b.
Three sides AB, BC and CA of a triangle ABC are 5x − 3y + 2 = 0, x − 3y − 2 = 0 and x + y − 6 = 0 respectively. Find the equation of the altitude through the vertex A.
Find the equation of the straight line passing through the point of intersection of the lines 5x − 6y − 1 = 0 and 3x + 2y + 5 = 0 and perpendicular to the line 3x − 5y + 11 = 0 .
The line 2x + 3y = 12 meets the x-axis at A and y-axis at B. The line through (5, 5) perpendicular to AB meets the x-axis and the line AB at C and E respectively. If O is the origin of coordinates, find the area of figure OCEB.
Find the length of the perpendicular from the origin to the straight line joining the two points whose coordinates are (a cos α, a sin α) and (a cos β, a sin β).
Find the length of the perpendicular from the point (4, −7) to the line joining the origin and the point of intersection of the lines 2x − 3y + 14 = 0 and 5x + 4y − 7 = 0.
Find the equations to the straight lines passing through the point (2, 3) and inclined at and angle of 45° to the line 3x + y − 5 = 0.
Find the equations to the sides of an isosceles right angled triangle the equation of whose hypotenues is 3x + 4y = 4 and the opposite vertex is the point (2, 2).
Find the equations of the two straight lines through (1, 2) forming two sides of a square of which 4x+ 7y = 12 is one diagonal.
The equation of the base of an equilateral triangle is x + y = 2 and its vertex is (2, −1). Find the length and equations of its sides.
If a, b, c are in A.P., then the line ax + by + c = 0 passes through a fixed point. Write the coordinates of that point.
Find the locus of the mid-points of the portion of the line x sinθ+ y cosθ = p intercepted between the axes.
A line passes through the point (2, 2) and is perpendicular to the line 3x + y = 3. Its y-intercept is
If the point (5, 2) bisects the intercept of a line between the axes, then its equation is
The inclination of the straight line passing through the point (−3, 6) and the mid-point of the line joining the point (4, −5) and (−2, 9) is
Find the equation of lines passing through (1, 2) and making angle 30° with y-axis.
In what direction should a line be drawn through the point (1, 2) so that its point of intersection with the line x + y = 4 is at a distance `sqrt(6)/3` from the given point.
A straight line moves so that the sum of the reciprocals of its intercepts made on axes is constant. Show that the line passes through a fixed point.
If a, b, c are in A.P., then the straight lines ax + by + c = 0 will always pass through ______.
The equation of the line joining the point (3, 5) to the point of intersection of the lines 4x + y – 1 = 0 and 7x – 3y – 35 = 0 is equidistant from the points (0, 0) and (8, 34).
