Advertisements
Advertisements
प्रश्न
c2 क्षेत्रफल के किसी दिए हुए गत्ते से वर्गाकार आधार का एक खुला हुआ बाक्स बनाना है। सिद्ध कीजिए कि बाक्स का महत्तम आयतन `c^3/(6sqrt3)` घन इकाई है।
उत्तर
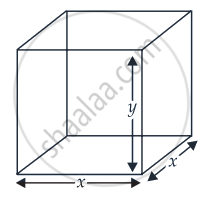
मान लीजिए x घनीय खुला बाक्स के वर्गाकार आधार की भुजा की लंबाई है और y इसकी ऊंचाई है।
∴ खुले बाक्स का पृष्ठीय क्षेत्रफल
c2 = x2 + 4xy
⇒ y = `("c"^2 - x^2)/(4x)` ....(i)
अब बाक्स का आयतन, V = x × x × y
⇒ V = x2y
⇒ V = `x^2(("c"^2 - x^2)/(4x))`
⇒ V = `1/4 ("c"^2x - x^3)`
दोनों पक्षों में अंतर करना w.r.t. x, हमें मिलता है
`"dv"/"dx" = 1/4 ("c"^2 - 3x^2)` ....(ii)
`"dV"/"dx"` = 0 स्थानीय उच्चिष्ठ और स्थानीय निम्निष्ठ के लिए,
∴ `1/4 ("c"^2 - 3x^2)` = 0
⇒ c2 – 3x2 = 0
⇒ x2 = `"c"^2/3`
∴ x = `sqrt("c"^2/3) = "c"/sqrt(3)`
अब पुन: विभेदित समीकरण (ii) w.r.t. x, हमें मिलता है
`("d"^2"V")/("dx"^2) = 1/4 (- 6x)`
= `(-3)/2 * "c"/sqrt(3) < 0` ...(उच्चिष्ठ)
घनीय बाक्स का आयतन (V) = x2y
= `x^2(("c"^2 - x^2)/4x)`
= `"c"/sqrt(3)[("c"^2 - "c"^2/3)/4]`
= `"c"/sqrt(3) xx (2"c"^2)/(3 xx 4)`
= `"c"^3/(6sqrt(3))`
अतः खुले बाक्स का अधिकतम आयतन `"c"^3/(6sqrt(3))` घन इकाई है।
APPEARS IN
संबंधित प्रश्न
अवकलज का प्रयोग करके निम्नलिखित में से सन्निकट मान ज्ञात कीजिए।
`(17/81)^(1/4)`
सिद्ध कीजिए कि फलन f(x) = 4x3 – 18x2 + 27x – 7 का कोई उच्चिष्ठ अथवा निम्निष्ठ नहीं है।
वक्र y = cos (x + y), –2π ≤ x ≤ 2π, की उन सभी स्पर्श रेखाओं के समीकरण ज्ञात कीजिए जो रेखा x + 2y = 0 के समांतर हैं।
सिद्ध कीजिए कि वक्र x = 3cos θ – cos3θ, y = 3sinθ – sin3θ के किसी बिंदु पर अभिंलब का समीकरण 4 (y cos3θ – x sin3θ) = 3 sin 4θ
वक्र `3"y" = 6"x" – 5"x"^3` पर स्थित उस बिंदु का भुज, जिस पर वक्र का अभिलंब मूल बिंदुसे होकर जाता है।
यदि f (x) = `1/(4x^2 + 2x + 1)`, तो इसका उच्चतम मान ______ है।
sinx + cosx का उच्चिष्ठ मान ______ है।
यदि किसी वृत्त का क्षेत्रफल एक समान दर से बढ़ता है, तो सिद्ध कीजिए कि उसका परिमाप (परिधि) उसकी त्रिज्या के व्युत्क्रमानुपाती होता है
कोण θ, 0 < θ < `π/2`, ज्ञात कीजिए जो अपने sine से दोगुनी तेजी से बढ़ता है।
(1.999)5 का सन्निकट मान ज्ञात कीजिए।
एक खोखले बेलनाकार खोल, जिसकी आंतरिक तथा बाह्य त्रिज्याएँ क्रमश: 3 cm तथा 3.0005 cm हैं, में धातु के आयतन का सन्निकट मान ज्ञात कीजिए।
वक्र `sqrt(x) + sqrt(y) = 4` उस बिंदु के निर्देशांक ज्ञात कीजिए, जिस पर स्पर्श रेखा का अक्षों से झुकाव समान है।
वक्र x2 + y2 – 2x – 4y + 1 = 0 के किन बिंदुओं पर स्पर्श रेखाएँ y-अक्ष के समांतर हैं।
सिद्ध किजिए कि f (x) = tan–1(sinx + cosx), अतंराल 0,`pi/4` में एक वर्धमान फलन है।
वर्गाकार आधार तथा ऊर्ध्वाधर पृष्ठ वाले धातु के किसी बाक्स में 1024 cm3 वस्तु आती है। शीर्ष तथा आधार के पृष्ठों के माल (वस्तु) का मूल्य Rs 5/cm2 है तथा पृष्ठों के मान का मूल्य Rs 2.50/cm2 हैं। बाक्स का निम्नतम मूल्य ज्ञात कीजिए।
भुजा x, 2x और `x/3` किसी आयताकार समांतर षट्फलक तथा एक गोले के पृष्ठीय क्षेत्रफल का योगफल अचर दिया हुआ है। सिद्ध कीजिए कि उनके आयतन का योगफल निम्नतम होगा, यदि x गोले की त्रिज्या के तीन गुने के बराबर है। उनके आयतन के योगफल का निम्नतम मान भी ज्ञात कीजिए।
एक क्षैतिज फर्श पर 5 मीटर लंबी एक सीढ़ी किसी ऊर्ध्वाधर दीवार पर झुकी है।यदि सीढ़ी का ऊपरी सिरा 10 cm/sec, की दर से नीचे की ओर फिसल रहा है तो सीढ़ी तथा फर्श के बीच का कोण, उस समय जब सीढ़ी का निचला सिरा दीवार से 2 मीटर दूर है:
वक्र y = e2x की, बिंदु (0, 1) पर, स्पर्श रेखा x-अक्ष से बिंदु ______
दो वक्र x3 – 3xy2 + 2 = 0 तथा 3x2 y – y3 – 2 = 0 किस कोण पर प्रतिच्छेद करते हैं:
मान लीजिए कि f : R → R, f (x) = 2x + cosx द्वारा परिभाषित है, तो f ______
y = x(x – 3)2, x के नीचे दिए हुए मानों के लिए हासमान है,
फलन f(x) = tanx – x ______
बहुपद x3 – 18x2 + 96x का, अंतराल [0, 9] में, निम्नतम मान ______
f (x) = 2 sin3x + 3 cos3x का मान x = `(5pi)/6`, पर ______
वक् y = –x3 + 3x2 + 9x – 27 की उच्चतम प्रवणता ______
फलन f(x) = `(2x^2 - 1)/x^4`, x > 0, अंतराल में ______ हासमान है।
