Advertisements
Advertisements
प्रश्न
Find one-parameter families of solution curves of the following differential equation:-
\[\left( x + y \right)\frac{dy}{dx} = 1\]
Solve the following differential equation:-
\[\left( x + y \right)\frac{dy}{dx} = 1\]
उत्तर
We have,
\[\left( x + y \right)\frac{dy}{dx} = 1\]
\[ \Rightarrow \frac{dy}{dx} = \frac{1}{x + y}\]
\[ \Rightarrow \frac{dx}{dy} = x + y\]
\[ \Rightarrow \frac{dx}{dy} - x = y . . . . . \left( 1 \right)\]
Clearly, it is a linear differential equation of the form
\[\frac{dx}{dy} + Px = Q\]
where
\[P = - 1\]
\[Q = y\]
\[ \therefore I . F . = e^{\int P\ dy} \]
\[ = e^{\int - 1 dy} \]
\[ = e^{- y} \]
\[\text{ Multiplying both sides of }(1)\text{ by }e^{- y} ,\text{ we get }\]
\[ e^{- y} \left( \frac{dx}{dy} - x \right) = e^{- y} y\]
\[ \Rightarrow e^{- y} \frac{dx}{dy} - e^{- y} x = e^{- y} y\]
Integrating both sides with respect to y, we get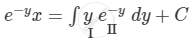
\[ \Rightarrow e^{- y} x = y\int e^{- y} dy - \int\left[ \frac{d}{dy}\left( y \right)\int e^{- y} dy \right]dy + C\]
\[ \Rightarrow e^{- y} x = - y e^{- y} - e^{- y} + C\]
\[ \Rightarrow e^{- y} x + y e^{- y} + e^{- y} = C\]
\[ \Rightarrow \left( x + y + 1 \right) e^{- y} = C\]
\[ \Rightarrow \left( x + y + 1 \right) = C e^y \]
\[\text{ Hence, }\left( x + y + 1 \right) = C e^y\text{ is the required solution.}\]
APPEARS IN
संबंधित प्रश्न
Form the differential equation of the family of circles touching the y-axis at the origin.
Form the differential equation of the family of ellipses having foci on y-axis and centre at origin.
Form the differential equation of the family of circles having centre on y-axis and radius 3 units.
Form the differential equation representing the family of curves given by (x – a)2 + 2y2 = a2, where a is an arbitrary constant.
Show that the family of curves for which `dy/dx = (x^2+y^2)/(2x^2)` is given by x2 - y2 = cx
Form the differential equation corresponding to y = emx by eliminating m.
Form the differential equation from the following primitive where constants are arbitrary:
xy = a2
Form the differential equation corresponding to y2 = a (b − x2) by eliminating a and b.
Form the differential equation of the family of curves represented by the equation (a being the parameter):
(2x + a)2 + y2 = a2
Form the differential equation of the family of curves represented by the equation (a being the parameter):
(2x − a)2 − y2 = a2
Find one-parameter families of solution curves of the following differential equation:-
\[\frac{dy}{dx} - y = \cos 2x\]
Find one-parameter families of solution curves of the following differential equation:-
\[x\frac{dy}{dx} + y = x^4\]
Find one-parameter families of solution curves of the following differential equation:-
\[\frac{dy}{dx} - \frac{2xy}{1 + x^2} = x^2 + 2\]
Find one-parameter families of solution curves of the following differential equation:-
\[\frac{dy}{dx} \cos^2 x = \tan x - y\]
Find one-parameter families of solution curves of the following differential equation:-
\[e^{- y} \sec^2 y dy = dx + x dy\]
Find one-parameter families of solution curves of the following differential equation:-
\[x \log x\frac{dy}{dx} + y = 2 \log x\]
Find one-parameter families of solution curves of the following differential equation:-
\[x\frac{dy}{dx} + 2y = x^2 \log x\]
Write the order of the differential equation representing the family of curves y = ax + a3.
The family of curves in which the sub tangent at any point of a curve is double the abscissae, is given by
Form the differential equation representing the family of curves y = mx, where m is an arbitrary constant.
Form the differential equation of the family of hyperbolas having foci on x-axis and centre at the origin.
Form the differential equation representing the family of curves `y2 = m(a2 - x2) by eliminating the arbitrary constants 'm' and 'a'.
Find the equation of a curve whose tangent at any point on it, different from origin, has slope `y + y/x`.
The differential equation representing the family of curves y = A sinx + B cosx is ______.
Find the equation of a curve passing through origin and satisfying the differential equation `(1 + x^2) "dy"/"dx" + 2xy` = 4x2
Find the equation of a curve passing through origin if the slope of the tangent to the curve at any point (x, y) is equal to the square of the difference of the abcissa and ordinate of the point.
Find the equation of a curve passing through the point (1, 1). If the tangent drawn at any point P(x, y) on the curve meets the co-ordinate axes at A and B such that P is the mid-point of AB.
Family y = Ax + A3 of curves is represented by the differential equation of degree ______.
The differential equation `y ("d"y)/("d"x) + "c"` represents: ______.
Family y = Ax + A3 of curves will correspond to a differential equation of order ______.
Differential equation representing the family of curves y = ex (Acosx + Bsinx) is `("d"^2y)/("d"x^2) - 2 ("d"y)/("d"x) + 2y` = 0
Find the equation of the curve at every point of which the tangent line has a slope of 2x:
The area above the x-axis and under the curve `y = sqrt(1/x - 1)` for `1/2 ≤ x ≤ 1` is:
