Advertisements
Advertisements
प्रश्न
Find the area of the triangle whose vertices are (-1, 1), (0, 5) and (3, 2), using integration.
उत्तर
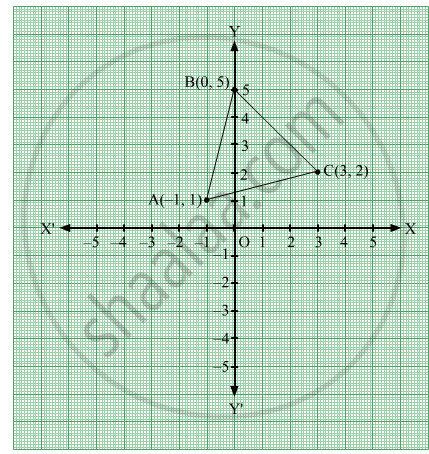
Let A (-1,1), B (0,5) and C (3,2)
The equation of line AB is
y -1 = `(5 -1)/(0+ 1) ("x"+1)`
y = `4"x" + 5`
The equation of line BC is
y - 5 = `(2 -5)/(3 -0) ("x" -0)`
y = `-"x"+5`
The equation of line CA is
y - 2 = `(1 -2)/(-1 -3) ("x" -3)`
y = `("x")/(4) + (5)/(4)`
Required area = Area of ΔABC
The equation of line CA is
y - 2 = `(1 -2)/(-1 -3) ("x" -3)`
y = `("x")/(4) + (5)/(4)`
Required area = Area of ΔABC
= `int_-1^0 (4x + 5) dx + int_0^3 (- x + 5) dx - int_-1^3 ( x/4 + 5/4) dx`
= `[ 2x^2 + 5x ]_-1^0 + [ -x^2/2 + 5x ]_0^3 - [ x^2/8 + 5x/4 ]_-1^3`
= `3 + 21/2 - 39/8 - 9/8`
= `15/2` sq. units
APPEARS IN
संबंधित प्रश्न
Evaluate :`int_(pi/6)^(pi/3) dx/(1+sqrtcotx)`
Find the integrals of the function:
sin 3x cos 4x
Find the integrals of the function:
sin3 (2x + 1)
Find the integrals of the function:
sin 4x sin 8x
Find the integrals of the function:
`(sin^2 x)/(1 + cos x)`
Find the integrals of the function:
`(cos 2x - cos 2 alpha)/(cos x - cos alpha)`
Find the integrals of the function:
`1/(sin xcos^3 x)`
`int (sin^2x - cos^2 x)/(sin^2 x cos^2 x) dx` is equal to ______.
`int (e^x(1 +x))/cos^2(e^x x) dx` equals ______.
Find `int dx/(x^2 + 4x + 8)`
Evaluate `int_0^(3/2) |x sin pix|dx`
Differentiate : \[\tan^{- 1} \left( \frac{1 + \cos x}{\sin x} \right)\] with respect to x .
Evaluate : \[\int\limits_0^\pi \frac{x \tan x}{\sec x \cdot cosec x}dx\] .
Find `int_ (sin "x" - cos "x" )/sqrt(1 + sin 2"x") d"x", 0 < "x" < π / 2 `
Find `int_ sin ("x" - a)/(sin ("x" + a )) d"x"`
Find `int_ (sin2"x")/((sin^2 "x"+1)(sin^2"x"+3))d"x"`
Find: `int_ (cos"x")/((1 + sin "x") (2+ sin"x")) "dx"`
Find: `intsqrt(1 - sin 2x) dx, pi/4 < x < pi/2`
Find `int "dx"/(2sin^2x + 5cos^2x)`
`int "e"^x (cosx - sinx)"d"x` is equal to ______.
`int (sin^6x)/(cos^8x) "d"x` = ______.
Evaluate the following:
`int ((1 + cosx))/(x + sinx) "d"x`
Evaluate the following:
`int sin^-1 sqrt(x/("a" + x)) "d"x` (Hint: Put x = a tan2θ)
`int (x + sinx)/(1 + cosx) "d"x` is equal to ______.
`int sinx/(3 + 4cos^2x) "d"x` = ______.
The value of the integral `int_(1/3)^1 (x - x^3)^(1/3)/x^4 dx` is
`int (cos^2x)/(sin x + cos x)^2 dx` is equal to
