Advertisements
Advertisements
प्रश्न
Find the temperature of a blackbody if its spectrum has a peak at (a) λmax = 700 nm (visible), (b) λmax = 3 cm (microwave region) (c) λmax = 3 m (short radio waves). (Take Wien’s constant b = 2.897 × 10-3 m.K).
उत्तर
Given: (a) λmax = 700 nm = 700 × 10-9 m,
(b) λmax = 3 cm = 3 × 10-2 m,
(c) λmax = 3 cm,
b = 2.897 × 10-3 m.K.
∴ λmax T = b
(a) T = `"b"/lambda_"max"`
`= (2.897 xx 10^-3 "m"."K")/(700 xx 10^-9 "m")`
`= (2.897 xx 10^-3)/(7 xx 10^-7)`
= 0.4138 × 104
= 4138 K
(b) T = `"b"/lambda_"max"`
`= (2.897 xx 10^-3 "m"."K")/(3 xx 10^-2 "m")`
`= (2.879 xx 10^-1 "K")/3`
= 0.966 × 10-1 K
= 0.0966 K
(c) T = `"b"/lambda_"max"`
`= (2.897 xx 10^-3 "m.K")/(3 " m")`
= 0.966 × 10-3 K
APPEARS IN
संबंधित प्रश्न
If the molecules were not allowed to collide among themselves, would you expect more evaporation or less evaporation?
Find the number of molecules of an ideal gas in a volume of 1.000 cm3 at STP.
A gas cylinder has walls that can bear a maximum pressure of 1.0 × 106 Pa. It contains a gas at 8.0 × 105 Pa and 300 K. The cylinder is steadily heated. Neglecting any change in the volume, calculate the temperature at which the cylinder will break.
The average translational kinetic energy of air molecules is 0.040 eV (1 eV = 1.6 × 10−19J). Calculate the temperature of the air. Boltzmann constant k = 1.38 × 10−23 J K−1.
The mean speed of the molecules of a hydrogen sample equals the mean speed of the molecules of a helium sample. Calculate the ratio of the temperature of the hydrogen sample to the temperature of the helium sample.
Use R = 8.314 JK-1 mol-1
During an experiment, an ideal gas is found to obey an additional law pV2 = constant. The gas is initially at a temperature T and volume V. Find the temperature when it expands to a volume 2V.
Use R = 8.3 J K-1 mol-1
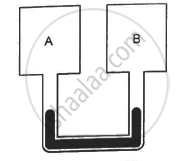
Figure shows two vessels A and B with rigid walls containing ideal gases. The pressure, temperature and the volume are pA, TA, V in the vessel A and pB, TB, V in the vessel B. The vessels are now connected through a small tube. Show that the pressure p and the temperature T satisfy `Ρ/T = 1/2 ({P_A}/{T_A}+{P_B}/{T_B))` when equilibrium is achieved.

An ideal gas is trapped between a mercury column and the closed-end of a narrow vertical tube of uniform base containing the column. The upper end of the tube is open to the atmosphere. The atmospheric pressure equals 76 cm of mercury. The lengths of the mercury column and the trapped air column are 20 cm and 43 cm respectively. What will be the length of the air column when the tube is tilted slowly in a vertical plane through an angle of 60°? Assume the temperature to remain constant.
One mole of an ideal gas undergoes a process `P = (P_0)/(1+(V/V_0)^2` where `p_0` and `V_0` are constants . Find the temperature of the gas when `V=V_0` .
The condition of air in a closed room is described as follows. Temperature = 25°C, relative humidity = 60%, pressure = 104 kPa. If all the water vapour is removed from the room without changing the temperature, what will be the new pressure? The saturation vapour pressure at 25°C − 3.2 kPa.
The temperature and the dew point in an open room are 20°C and 10°C. If the room temperature drops to 15°C, what will be the new dew point?
Figure shows two rigid vessels A and B, each of volume 200 cm3, containing an ideal gas (Cv = 12.5 J K−1 mol−1). The vessels are connected to a manometer tube containing mercury. The pressure in both the vessels is 75 cm of mercury and the temperature is 300 K. (a) Find the number of moles of the gas in each vessel. (b) 5.0 J of heat is supplied to the gas in vessel A and 10 J to the gas in vessel B. Assuming there's no appreciable transfer of heat from A to B, calculate the difference in the heights of mercury in the two sides of the manometer. Gas constant, R = 8.3 J K−1 mol−1.
A glass contains some water at room temperature 20°C. Refrigerated water is added to it slowly. when the temperature of the glass reaches 10°C, small droplets condense on the outer surface. Calculate the relative humidity in the room. The boiling point of water at a pressure of 17.5 mm of mercury is 20°C and at 8.9 mm of mercury it is 10°C.
An adiabatic cylindrical tube of cross-sectional area 1 cm2 is closed at one end and fitted with a piston at the other end. The tube contains 0.03 g of an ideal gas. At 1 atm pressure and at the temperature of the surrounding, the length of the gas column is 40 cm. The piston is suddenly pulled out to double the length of the column. The pressure of the gas falls to 0.355 atm. Find the speed of sound in the gas at atmospheric temperature.
Energy is emitted from a hole in an electric furnace at the rate of 20 W when the temperature of the furnace is 727°C. What is the area of the hole? (Take Stefan’s constant σ to be 5.7 × 10-8 Js-1 m-2K-4.)
The number of degrees of freedom, for the vibrational motion of a polyatomic molecule, depends on the ______
Why the temperature of all bodies remains constant at room temperature?
What is the microscopic origin of temperature?
The average translational kinetic energy of a molecule in a gas becomes equal to 0.49 eV at a temperature about (Boltzmann constant = 1.38 x 10-23 JK-1) ____________.
An ideal gas in a container of volume 500 cc is at a pressure of 2 × 105 N/m2. The average kinetic energy of each molecule is 6 × 10−21 J. The number of gas molecules in the container is ______.
Explain why there is no atmosphere on moon.
23Ne decays to 23Na by negative beta emission. Mass of 23Ne is 22.994465 amu mass of 23Na is 22.989768 amu. The maximum kinetic energy of emitted electrons neglecting the kinetic energy of recoiling product nucleus is ______ MeV.
The Q-value of a nuclear reaction and kinetic energy of the projectile particle, KP are related as ______.
When a particle oscillates simple harmonically, its kinetic energy varies periodically. If frequency of the particle is n, then the frequency of the kinetic energy is ______.
If a = 0. 72 and t = 0.04, then the value of r is ______.
At what temperature will therms velocity of a gas be four times its value at STP?
Show that the average energy per molecule is proportional to the absolute temperature T of the gas.
