Question

If the circles x² + y² = a and x² + y² − 6x − 8y + 9 = 0, touch externally, then a =

पर्याय

• 1

• -1

• 21

• 16

Answer 1

1

x² + y² = a        ...(1)
And, x² + y² − 6x − 8y + 9 = 0     ...(2)

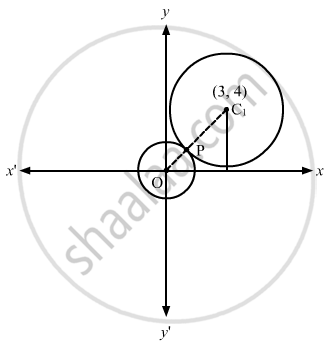
Let circles (1) and (2) touch each other at point P.
The centre of the circle x² + y² = a, O, is (0, 0).
The centre of the circle x² + y² − 6x − 8y + 9 = 0, C₁, is (3, 4).
Also, radius of circle (1) = \[\sqrt{a}\] =OP 

Radius of circle (2) = \[\sqrt{9 + 16 - 9} = 4\] =C₁P

From figure, we have:

\[C_1 O = C_1 P + OP\]

\[ \Rightarrow \sqrt{3^2 + 4^2} = 4 + \sqrt{a}\]

\[ \Rightarrow 5 = 4 + \sqrt{a}\]

\[ \Rightarrow a = 1\]