Advertisements
Advertisements
प्रश्न
If cos θ=0.6 show that (5sin θ -3tan θ) = 0
उत्तर
Let us consider a right ΔABC right angled at B.
Now, we know that cos θ = 0.6 = `(BC)/(AC) = 3/5`
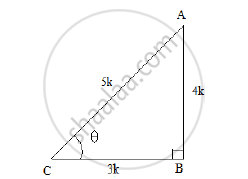
So, if BC = 3k, then AC = 5k, where k is a positive number.
Using Pythagoras theorem, we have:
`Ac^2 = AB^2 + BC^2`
`⟹ AB^2 = AC^2 − BC^2`
`⟹ AB^2 = (5K)^2 − (3K)^2 = 25K^2 − 9K^2`
`⟹ AB^2 = 16K^2`
⟹ 𝐴𝐵 = 4𝑘
Finding out the other T-rations using their definitions, we get:
sin θ = `(AB)/(AC) = (4K)/(5K) = 4/5`
TAN θ = `(AB)/(BC) = (4K)/(3K) = 4/3`
Substituting the values in the given expression, we get:
5 sin 𝜃 − 3 tan 𝜃
`⇒ 5 (4/5) - 3(4/3)`
= 4-4=0= RHS
i.e., LHS = RHS
Hence, Proved.
APPEARS IN
संबंधित प्रश्न
If 2θ + 45° and 30° − θ are acute angles, find the degree measure of θ satisfying Sin (20 + 45°) = cos (30 - θ°)
If cosec θ= 2 show that `(cot θ +sin θ /(1+cos θ )) =2`
If 3 cot `theta = 2, `show that `((4 sin theta - 4 cos theta))/((2 sin theta + 6 cos theta ))=1/3`
If A = 450, verify that :
(i) sin 2A = 2 sin A cos A
If sin (A – B) = `1/2` and cos (A + B) = `1/2, 0^0 ≤ (A + B) ≤ 90^0` and A > B, then find A and B.
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
cose C = `(15)/(11)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
tan C = `(5)/(12)`
In each of the following, one trigonometric ratio is given. Find the values of the other trigonometric.
sec B = `(15)/(12)`
From the given figure, find the values of tan C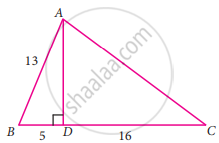
Assertion (A): For 0 < 0 ≤ 90°, cosec θ – cot θ and cosec θ + cot θ are reciprocal of each other.
Reason (R): cot2 θ – cosec2 θ = 1.
