Advertisements
Advertisements
प्रश्न
If sin α = `1/2`, then find the value of (3 cos α – 4 cos3 α).
उत्तर
Given that,
sin α = `1/2`
So, sin α = sin 30° = `1/2`
`\implies` α = 30°
Now, (3 cos α – 4 cos3 α)
= (3 cos 30° – 4 cos3 30°)
= `(3 xx sqrt(3)/2 - 4 xx (sqrt(3)/2)^3)`
= `(3sqrt(3))/2 - (3sqrt(3))/2`
= 0
APPEARS IN
संबंधित प्रश्न
Evaluate the following:
2tan2 45° + cos2 30° − sin2 60°
Evaluate the following
`sec 11^@/(cosec 79^@)`
Evaluate the following :
`((sin 49^@)/(cos 41^@))^2 + (cos 41^@/(sin 49^@))^2`
If A, B, C are the interior angles of a triangle ABC, prove that
`tan ((C+A)/2) = cot B/2`
Prove the following :
`(cos(90^@ - theta) sec(90^@ - theta)tan theta)/(cosec(90^@ - theta) sin(90^@ - theta) cot (90^@ - theta)) + tan (90^@ - theta)/cot theta = 2`
prove that:
tan (2 x 30°) = `(2 tan 30°)/(1– tan^2 30°)`
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratio: cos 45°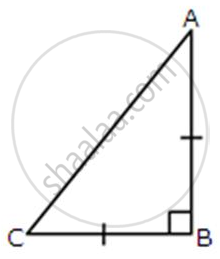
Prove that : sec245° - tan245° = 1
Find the value of x in the following: tan x = sin45° cos45° + sin30°
If A = B = 45°, verify that sin (A - B) = sin A .cos B - cos A.sin B
