Advertisements
Advertisements
प्रश्न
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(i) f + g
उत्तर
Given:
\[f\left( x \right) = \sqrt{x + 1}\text{ and } g\left( x \right) = \sqrt{9 - x^2}\]
Clearly,
Thus, domain (f) = [1, ∞]
Again,
⇒ \[x \in \left[ - 3, 3 \right]\]
APPEARS IN
संबंधित प्रश्न
A function f : R → R is defined by f(x) = x2. Determine (a) range of f, (b) {x : f(x) = 4}, (c) [y: f(y) = −1].
Let f : R+ → R, where R+ is the set of all positive real numbers, such that f(x) = loge x. Determine
(c) whether f(xy) = f(x) : f(y) holds
Let X = {1, 2, 3, 4} and Y = {1, 5, 9, 11, 15, 16}
Determine which of the set are functions from X to Y.
(a) f1 = {(1, 1), (2, 11), (3, 1), (4, 15)}
If f(x) = (x − a)2 (x − b)2, find f(a + b).
If \[y = f\left( x \right) = \frac{ax - b}{bx - a}\] , show that x = f(y).
Let f and g be two real functions defined by \[f\left( x \right) = \sqrt{x + 1}\] and \[g\left( x \right) = \sqrt{9 - x^2}\] . Then, describe function:
(iv) \[\frac{f}{g}\]
If f, g and h are real functions defined by
Let f(x) = x2 and g(x) = 2x+ 1 be two real functions. Find (f + g) (x), (f − g) (x), (fg) (x) and \[\left( \frac{f}{g} \right) \left( x \right)\] .
Write the range of the function f(x) = ex−[x], x ∈ R.
Let A = {1, 2, 3} and B = {2, 3, 4}. Then which of the following is a function from A to B?
If 2f (x) − \[3f\left( \frac{1}{x} \right) = x^2\] (x ≠ 0), then f(2) is equal to
Let A = {x ∈ R : x ≠ 0, −4 ≤ x ≤ 4} and f : A ∈ R be defined by \[f\left( x \right) = \frac{\left| x \right|}{x}\] for x ∈ A. Then th (is
Check if the following relation is function:

A function f is defined as follows: f(x) = 5 − x for 0 ≤ x ≤ 4. Find the value of x such that f(x) = 3
Check if the following relation is a function.
Find x, if g(x) = 0 where g(x) = 6x2 + x − 2
Express the following logarithmic equation in exponential form
log2 64 = 6
If f(x) = ax2 − bx + 6 and f(2) = 3 and f(4) = 30, find a and b
If f(x) = 3x + 5, g(x) = 6x − 1, then find (f − g) (2)
Select the correct answer from given alternatives.
Find x, if 2log2 x = 4
The equation logx2 16 + log2x 64 = 3 has,
Answer the following:
If `log (("a" + "b")/2) = 1/2(log"a" + log"b")`, then show that a = b
Answer the following:
If `log ((x - y)/5) = 1/2 logx + 1/2 log y`, show that x2 + y2 = 27xy
Answer the following:
Find value of `(3 + log_10 343)/(2 + 1/2 log_10 (49/4) + 1/2 log_10 (1/25)`
Answer the following:
If `log"a"/(x + y - 2z) = log"b"/(y + z - 2x) = log"c"/(z + x - 2y)`, show that abc = 1
Answer the following:
Show that, logy x3 . logz y4 . logx z5 = 60
A graph representing the function f(x) is given in it is clear that f(9) = 2
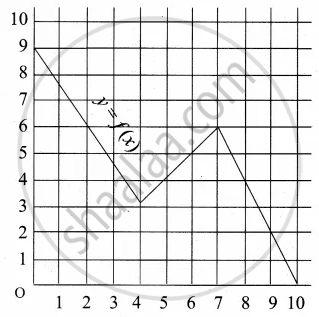
Describe the following Range
If f(x) = `(x - 1)/(x + 1), x ≠ - 1` Show that f(f(x)) = `- 1/x`, Provided x ≠ 0
The domain of the real valued function f(x) = `sqrt((x - 2)/(3 - x))` is ______.
If a function f(x) is given as f(x) = x2 – 6x + 4 for all x ∈ R, then f(–3) = ______.
Find the range of the following functions given by `sqrt(16 - x^2)`
Find the domain of the following functions given by f(x) = x|x|
Let f(x) = `sqrt(x)` and g(x) = x be two functions defined in the domain R+ ∪ {0}. Find (fg)(x)
Find the domain and range of the function f(x) = `1/sqrt(x - 5)`
The domain of the function f given by f(x) = `(x^2 + 2x + 1)/(x^2 - x - 6)` is ______.
If f(x) = x3 – 1 and domain of f = {0, 1, 2, 3}, then domain of f–1 is ______.
The function f: R `rightarrow` R defined by f(x) = sin x is ______.
If f : R – {2} `rightarrow` R i s a function defined by f(x) = `(x^2 - 4)/(x - 2)`, then its range is ______.
Range of the function f(x) = `x/(1 + x^2)` is ______.
