Advertisements
Advertisements
प्रश्न
यदि cos(α + β) = `4/5` और sin(α - β) = `5/13` है; जहाँ α, 0 और `π/4` के बीच स्थित है; तो tan2α का मान ज्ञात कीजिए।
[संकेत: tan2α को tan(α + β + α - β) के रूप में व्यक्त कीजिए।]
उत्तर
tan(α + β) और tan(α - β) का मान ज्ञात कीजिए
निम्न आरेख में देख सकते हैं,
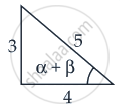
∵ cos(α + β) = `4/5`
∴ tan(α + β) = `3/4`
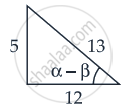
∵ sin(α - β) = `5/13`
∴ tan(α - β) = `5/12`
tan2α को tan(α + β + α – β) के रूप मे अभिव्यक्त करने पर
tan2α = tan(α + β + α – β)
= tan[(α + β) + (α – β)]
= tan(A + B) = `(tanA + tanB)/(1 - tanA.tanB)` लागू करने पर
tan2α = `(tan(alpha + beta) + tan(alpha - beta))/(1 - tan(alpha + beta)tan(alpha - beta))`
= `(3/4 + 5/12)/(1 - 3/4 xx 5/12)`
LCM लेने पर,
tan2α = `((9 + 5)/12)/((48 - 15)/48)`
= `14/12 xx 48/33`
= `56/33`
आवश्यक मान tan 2α = `56/33`.
APPEARS IN
संबंधित प्रश्न
`sqrt(3)` cosec 20° – sec 20° का मान ज्ञात कीजिए।
sin θ + sin 3θ + sin 5θ = 0 को हल कीजिए।
`(1 + cos pi/8)(1 + cos (3pi)/8)(1 + cos (5pi)/8)(1 + cos (7pi)/8)` का मान ज्ञात कीजिए।
यदि कोण θ को ऐसे भागों में विभाजित किया जाता है कि एक भाग का tangent दूसरे भाग के tangent का k गुना है, तथा इन भागों का अंतर φ है, तो सिद्ध कीजिए कि sinθ = `(k + 1)/(k - 1) sinφ`
`sqrt(3)` cos θ + sin θ = `sqrt(2)` को हल कीजिए।
यदि tan θ = `(-4)/3` है, तो sinθ है
sinx cosx का अधिकतम मान है:
स्तंभ C1 में दिए प्रत्येक प्रविष्ट की स्तंभ C2 में दी गई प्रविष्टियों से मिलान कीजिए:
| C1 | C2 |
| (a) `(1 - cosx)/sinx` | (i) `cot^2 x/2` |
| (b) `(1 + cosx)/(1 - cosx)` | (ii) `cot x/2` |
| (c) `(1 + cosx)/sinx` | (iii) `|cos x + sin x|` |
| (d) `sqrt(1 + sin 2x)` | (iv) `tan x/2` |
सिद्ध कीजिए कि `(tanA + secA - 1)/(tanA - secA + 1) = (1 + sinA)/cosA`
यदि m sinθ = n sin(θ + 2α) है, तो सिद्ध कीजिए कि tan(θ + α)cotα = `(m + n)/(m - n)`
`["संकेत:" (sin(theta + 2alpha))/sintheta = m/n "लिखकर योगांतरानुपात का प्रयोग कीजिए।"]`
सिद्ध कीजिए कि cosθ `cos theta/2 - cos 3theta cos (9theta)/2` = sin7θ sin8θ है।
`["संकेत:" "L.H.S." = 1/2[2costheta cos theta/2 - 2 cos 3theta cos (9theta)/2] "के रूप में व्यक्त कीजिए।"]`
सिद्ध कीजिए कि sin4A = 4sinA cos3A - 4cosA sin3A है।
यदि tanθ + sinθ = m और tanθ - sinθ = n हो, तो सिद्ध कीजिए कि m2 - n2 = 4sinθ tanθ है।
[संकेत: m + n = 2tanθ, m - n = 2sinθ है। तो m2 - n2 = (m + n) (m - n) का प्रयोग कीजिए।]
यदि tan(A + B) = p और tan(A - B) = q है, तो सिद्ध कीजिए कि
यदि cosα + cosβ = 0 = sinα + sinβ है, तो सिद्ध कीजिए कि cos2α + cos2β = -2cos(α + β) है।
व्यंजक `3[sin^4 ((3pi)/2 - alpha) + sin^4 (3pi + alpha)] - 2[sin^6 (pi/2 + alpha) + sin^6 (5pi - alpha)]` का मान ज्ञात कीजिए।
यदि θ प्रथम चतुर्थांश में स्थित है तथा `costheta = 8/17` है, तो cos(30° + θ) + cos(45° - θ) + cos(120° - θ) का मान ज्ञात कीजिए।
व्यंजक `cos^4 pi/8 + cos^4 (3pi)/8 + cos^4 (5pi)/8 + cos^4 (7pi)/8` का मान ज्ञात कीजिए।
[संकेत: व्यंजक `2(cos^4 pi/8 + cos^4 (3pi)/8) = 2[(cos^2 pi/8 + cos^2 (3pi)/8)^2 - 2cos^2 pi/8 cos^2 (3pi)/8]` के रूप में सरल कीजिए।
यदि tanθ = 3 है और θ तीसरे चतुर्थांश में स्थित है, तो sinθ का मान है।
cos2θ cos2Φ + sin2(θ - Φ) - sin2(θ + Φ) बराबर है।
[संकेत: sin2A - sin2B = sin(A + B) sin(A - B) का प्रयोग कीजिए।]
यदि x की सभी वास्तविक मान के लिए, `cosθ = x + 1/x` है, तो ______
`(sin 50^circ)/(sin 130^circ)` का मान ______ है।
यदि sinx + cosx = a, तो sin6x + cos6x = ______
यदि sinx + cosx = a, तो |sinx - cosx| = ______
