Advertisements
Advertisements
Question
A 6⋅5 m long ladder rests against a vertical wall reaching a height of 6⋅0 m. A 60 kg man stands half way up the ladder.
- Find the torque of the force exerted by the man on the ladder about the upper end of the ladder.
- Assuming the weight of the ladder to be negligible as compared to the man and assuming the wall to be smooth, find the force exerted by the ground on the ladder.
Solution
Given
Mass of the man = m = 60 kg
Ladder length = 6.5 m
Height of the wall = 6 m
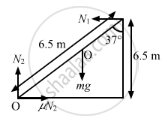
(a) We have to find the torque due to the weight of the body about the upper end of the ladder.
\[\tau = 60 \times 10 \times \frac{6 . 5}{2}\sin\theta\]
\[ \Rightarrow \tau = 600 \times \frac{6 . 5}{2} \times \sqrt{\left( 1 - \cos^2 \theta \right)}\]
\[ \Rightarrow \tau = 600 \times \left( \frac{6 . 5}{2} \right) \times \sqrt{\left\{ 1 - \left( \frac{6}{6 . 5} \right)^2 \right\}}\]
\[ \Rightarrow \tau = 740 N - m\]
(b) Let us find the vertical force exerted by the ground on the ladder.
\[N_2 = mg = 60 \times 9 . 8 = 588 N\]
Vertical force exerted by the ground on the ladder = \[\mu N_2 = N_1\]
As system is in rotational equilibrium, we have
\[\tau_{\text{net}} = 0 ............\left(\text{about O} \right)\]
\[\Rightarrow 6 . 5 N_1 \cos\theta = 60g \times \frac{6 . 5}{2}\sin\theta\]
\[\Rightarrow N_1 = \frac{1}{2}60g\tan\theta\]
\[= \frac{1}{2}60g \times \left( \frac{2 . 5}{6} \right) ...........\left[\text{using, }\tan\theta = \frac{2.5}{6} \right]\]
\[ \Rightarrow N_1 = \frac{25}{2}g\]
\[ \Rightarrow N_1 = 122 . 5 N \approx 120 N\]
APPEARS IN
RELATED QUESTIONS
Find the components along the x, y, z axes of the angular momentum l of a particle, whose position vector is r with components x, y, z and momentum is p with components px, py and 'p_z`. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s–1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of the angular momentum of the cylinder about its axis?
Explain why friction is necessary to make the disc in Figure roll in the direction indicated
(a) Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins?
The torque of a force \[\overrightarrow F \] about a point is defined as \[\overrightarrow\Gamma = \overrightarrow r \times \overrightarrow F.\] Suppose \[\overrightarrow r, \overrightarrow F\] and \[\overrightarrow \Gamma\] are all nonzero. Is \[r \times \overrightarrow\Gamma || \overrightarrow F\] always true? Is it ever true?
If the resultant torque of all the forces acting on a body is zero about a point, is it necessary that it will be zero about any other point?
A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.
Equal torques act on the disc A and B of the previous problem, initially both being at rest. At a later instant, the linear speeds of a point on the rim of A and another point on the rim of B are \[\nu_A\] and \[\nu_B\] respectively. We have
The density of a rod gradually decreases from one end to the other. It is pivoted at an end so that it can move about a vertical axis though the pivot. A horizontal force F is applied on the free end in a direction perpendicular to the rod. The quantities, that do not depend on which end of the rod is pivoted, are ________________ .
A particle of mass m is projected with a speed u at an angle θ with the horizontal. Find the torque of the weight of the particle about the point of projection when the particle is at the highest point.
When a force of 6⋅0 N is exerted at 30° to a wrench at a distance of 8 cm from the nut it is just able to loosen the nut. What force F would be sufficient to loosen it if it acts perpendicularly to the wrench at 16 cm from the nut?

Calculate the total torque acting on the body shown in the following figure about the point O.

A flywheel of moment of inertia 5⋅0 kg-m2 is rotated at a speed of 60 rad/s. Because of the friction at the axle it comes to rest in 5⋅0 minutes. Find (a) the average torque of the friction (b) the total work done by the friction and (c) the angular momentum of the wheel 1 minute before it stops rotating.
A particle of mass 5 units is moving with a uniform speed of v = `3sqrt 2` units in the XOY plane along the line y = x + 4. Find the magnitude of angular momentum
The net external torque on a system of particles about an axis is zero. Which of the following are compatible with it?
- The forces may be acting radially from a point on the axis.
- The forces may be acting on the axis of rotation.
- The forces may be acting parallel to the axis of rotation.
- The torque caused by some forces may be equal and opposite to that caused by other forces.
Angular momentum of a single particle moving with constant speed along the circular path ______.
The magnitude of the torque on a particle of mass 1 kg is 2.5 Nm about the origin. If the force acting on it is 1 N, and the distance of the particle from the origin is 5 m, the angle between the force and the position vector is (in radians) ______.
A solid sphere is rotating in free space. If the radius of the sphere is increased while keeping the mass the same, which one of the following will not be affected?
