Advertisements
Advertisements
Question
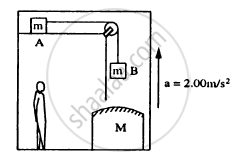
Consider the situation shown in figure. The elevator is going up with an acceleration of 2.00 m s−2 and the focal length of the mirror is 12.0 cm. All the surfaces are smooth and the pulley is light. The mass-pulley system is released from rest (with respect to the elevator) at t = 0 when the distance of B from the mirror is 42.0 cm. Find the distance between the image of the block B and the mirror at t = 0.200 s. Take g = 10 m s−2.
Solution
Given,
Acceleration of the elevator, a = 2.00 m/s2
Focal length of the mirror M, f = 12.00 cm
Acceleration due to gravity, g = 10 m/s2
Mass of blocks A and B = m
As per the question, the mass–pulley system is released at time t = 0.
Let the acceleration of the masses A and B with respect to the elevator be a.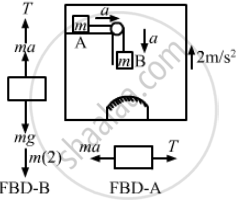
Using the free body diagram,
T − mg + ma − 2m = 0 ...(i)
Also,
T − ma = 0 ...(ii)
From (i) and (ii), we get:
2ma = m(g + 2)
`⇒ a = (10 + 2)/2`
`= 12/2 = 6 ms^-2`
Now, the distance travelled by block B of mass m in time t = 0.2 s is given by
`s = ut + 1/2at^2`
As `(u = 0)`
`s = 1/2 at^2`
On putting the respective values, we get:
`s = 1/2 xx 6 xx (0.2)^2`
`= 0.12 m = 12 cm`
As given in the question, the distance of block B from the mirror is 42 cm.
Object distance u from the mirror = − (42 − 12) = − 30 cm Using the mirror equation,
`1/v + 1/u = 1/f`
On putting the respective values, we get:
`1/v + 1/-30 = 1/12`
⇒ `1/v= 1/-30 = 1/ 12 + 1/30`
⇒ `v = 8.57 cm `
Hence, the distance between block B and mirror M is 8.57 cm.
APPEARS IN
RELATED QUESTIONS
A small candle, 2.5 cm in size is placed at 27 cm in front of a concave mirror of radius of curvature 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?
A double convex lens is made of a glass of refractive index 1.55, with both faces of the same radius of curvature. Find the radius of curvature required, if the focal length is 20 cm.
In motor vehicles, a convex mirror is attached near the driver's seat to give him the view of the traffic behind. What is the special function of this convex mirror which a plane mirror can not do?
If an object far away from a convex mirror moves towards the mirror, the image also moves. Does it move faster, slower or at the same speed as compared to the object?
In image formation from spherical mirrors, only paraxial rays are considered because they
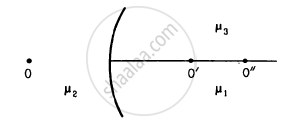
Following figure shows three transparent media of refractive indices \[\mu_1 , \mu_2 \text{ and } \mu_3\]. A point object O is placed in the medium \[\mu_2\]. If the entire medium on the right of the spherical surface has refractive index \[\mu_3\], the image forms at O". In the situation shown,
A man uses a concave mirror for shaving. He keeps his face at a distance of 25 cm from the mirror and gets an image which is 1.4 times enlarged. Find the focal length of the mirror.
A spherical surface of radius 30 cm separates two transparent media A and B with refractive indices 1.33 and 1.48 respectively. The medium A is on the convex side of the surface. Where should a point object be placed in medium A so that the paraxial rays become parallel after refraction at the surface?
A narrow pencil of parallel light is incident normally on a solid transparent sphere of radius r. What should be the refractive index is the pencil is to be focussed (a) at the surface of the sphere, (b) at the centre of the sphere.
How can the spherical aberration produced by a lens be minimized?
Answer the following question.
Under what conditions is the phenomenon of total internal reflection of light observed? Obtain the relation between the critical angle of incidence and the refractive index of the medium.
Answer the following question.
Three lenses of focal length +10 cm, —10 cm and +30 cm are arranged coaxially as in the figure given below. Find the position of the final image formed by the combination.

According to Cartesian sign convention, all distances are measured from the _______.
The focal length of a convex lens made of glass of refractive index (1.5) is 20 cm.
What will be its new focal length when placed in a medium of refractive index 1.25?
Is focal length positive or negative? What does it signify?
A parallel beam of light ray parallel to the x-axis is incident on a parabolic reflecting surface x = 2by2 as shown in the figure. After reflecting it passes through focal point F. What is the focal length of the reflecting surface?
A car is moving with at a constant speed of 60 km h–1 on a straight road. Looking at the rear view mirror, the driver finds that the car following him is at a distance of 100 m and is approaching with a speed of 5 km h–1. In order to keep track of the car in the rear, the driver begins to glance alternatively at the rear and side mirror of his car after every 2 s till the other car overtakes. If the two cars were maintaining their speeds, which of the following statement (s) is/are correct?
An object is 20 cm away from a concave mirror and it is within the focal length of the mirror. If the mirror is changed to a plane mirror, the image moves 15 cm closer to the mirror.
Focal length of the concave mirror is ______.
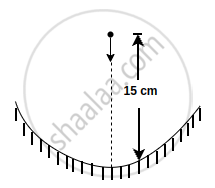
A particle is dropped along the axis from a height 15 cm on a concave mirror of focal length 30 cm as shown in figure. The acceleration due to gravity is 10 m/s2. Find the maximum speed of image in m/s:
A converging lens has a focal length of 10 cm in air. It is made of a material with a refractive index of 1.6. If it is immersed in a liquid of refractive index 1.3, find its new focal length.
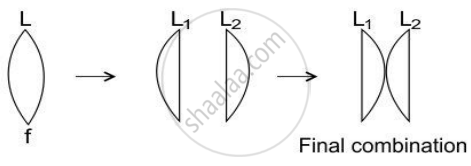
A lens of focal length f is divided into two equal parts and then these parts are put in a combination as shown in the figure below.
- What is the focal length of L1?
- What is the focal length of the final combination?