Question

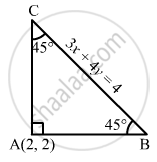
Find the equations to the sides of an isosceles right angled triangle the equation of whose hypotenues is 3x + 4y = 4 and the opposite vertex is the point (2, 2).

Answer 1

\[Here , we are given \bigtriangleup ABC is an isosceles right angled triangle . \]

\[\angle A + \angle B + \angle C = 180^\circ\]

\[ \Rightarrow 90^\circ + \angle B + \angle B = 180^\circ\]

\[ \Rightarrow \angle B = 45^\circ, \angle C = 45^\circ\]

Now, we have to find the equations of the sides AB and AC, where 3x + 4y = 4 is the equation of the hypotenuse BC.

We know that the equations of two lines passing through a point \[\left( x_1 , y_1 \right)\] and making an angle \[\alpha\] with the given line y = mx + c are \[y - y_1 = \frac{m \pm \tan\alpha}{1 \mp m\tan\alpha}\left( x - x_1 \right)\]

Here,

Equation of the given line is, 

\[3x + 4y = 4\]

\[ \Rightarrow 4y = - 3x + 4\]

\[ \Rightarrow y = - \frac{3}{4}x + 1\]

\[\text { Comparing this equation with } y = mx + c\]

we get, 

\[m = - \frac{3}{4}\]

\[x_1 = 2, y_1 = 2, \alpha = {45}^\circ , m = - \frac{3}{4}\]

So, the equations of the required lines are

\[y - 2 = \frac{- \frac{3}{4} + \tan {45}^\circ}{1 + \frac{3}{4}\tan {45}^\circ}\left( x - 2 \right)\text {  and } y - 2 = \frac{- \frac{3}{4} - \tan {45}^\circ}{1 - \frac{3}{4}\tan {45}^\circ}\left( x - 2 \right)\]

\[ \Rightarrow y - 2 = \frac{- \frac{3}{4} + 1}{1 + \frac{3}{4}}\left( x - 2 \right) \text { and } y - 2 = \frac{- \frac{3}{4} - 1}{1 - \frac{3}{4}}\left( x - 2 \right)\]

\[ \Rightarrow y - 2 = \frac{1}{7}\left( x - 2 \right) \text { and } y - 2 = \frac{- 7}{1}\left( x - 2 \right)\]

\[ \Rightarrow x - 7y + 12 = 0\text {  and } 7x + y - 16 = 0\]