Advertisements
Advertisements
Question
Find the points on the curve y = x3 at which the slope of the tangent is equal to the y-coordinate of the point.
Solution
The equation of the given curve is y = x3.
`:. dy/dx = 3x^2`
The slope of the tangent at the point (x, y) is given by,
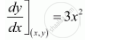
When the slope of the tangent is equal to the y-coordinate of the point, then y = 3x2.
Also, we have y = x3.
∴3x2 = x3
⇒ x2 (x − 3) = 0
⇒ x = 0, x = 3
When x = 0, then y = 0 and when x = 3, then y = 3(3)2 = 27.
Hence, the required points are (0, 0) and (3, 27).
APPEARS IN
RELATED QUESTIONS
Show that the equation of normal at any point t on the curve x = 3 cos t – cos3t and y = 3 sin t – sin3t is 4 (y cos3t – sin3t) = 3 sin 4t
Find the slope of the tangent to curve y = x3 − x + 1 at the point whose x-coordinate is 2.
Find the slope of the tangent to the curve y = x3 − 3x + 2 at the point whose x-coordinate is 3.
The slope of the normal to the curve y = 2x2 + 3 sin x at x = 0 is
(A) 3
(B) 1/3
(C) −3
(D) `-1/3`
Find the points on the curve y = `4x^3 - 3x + 5` at which the equation of the tangent is parallel to the x-axis.
Find the slope of the tangent and the normal to the following curve at the indicted point y = x3 − x at x = 2 ?
Find the slope of the tangent and the normal to the following curve at the indicted point x = a (θ − sin θ), y = a(1 − cos θ) at θ = −π/2 ?
Find the points on the curve y = 3x2 − 9x + 8 at which the tangents are equally inclined with the axes ?
Find the points on the curve x2 + y2 = 13, the tangent at each one of which is parallel to the line 2x + 3y = 7 ?
Find the equation of the tangent and the normal to the following curve at the indicated point \[\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \text { at } \left( a\sec\theta, b\tan\theta \right)\] ?
Find the equation of the tangent and the normal to the following curve at the indicated point y2 = 4ax at \[\left( \frac{a}{m^2}, \frac{2a}{m} \right)\] ?
Find the equation of the tangent and the normal to the following curve at the indicated point xy = c2 at \[\left( ct, \frac{c}{t} \right)\] ?
Find the equation of the tangent and the normal to the following curve at the indicated point \[\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \text { at } \left( x_0 , y_0 \right)\] ?
Find the equation of the tangent and the normal to the following curve at the indicated points x = θ + sinθ, y = 1 + cosθ at θ = \[\frac{\pi}{2}\] ?
Find the equation of the tangent and the normal to the following curve at the indicated points \[x = \frac{2 a t^2}{1 + t^2}, y = \frac{2 a t^3}{1 + t^2}\text { at } t = \frac{1}{2}\] ?
The equation of the tangent at (2, 3) on the curve y2 = ax3 + b is y = 4x − 5. Find the values of a and b ?
Find the equation of the tangent line to the curve y = x2 − 2x + 7 which is parallel to the line 2x − y + 9 = 0 ?
Find the angle of intersection of the following curve y2 = x and x2 = y ?
Find the angle of intersection of the following curve x2 = 27y and y2 = 8x ?
Write the coordinates of the point on the curve y2 = x where the tangent line makes an angle \[\frac{\pi}{4}\] with x-axis ?
Write the equation on the tangent to the curve y = x2 − x + 2 at the point where it crosses the y-axis ?
Write the angle between the curves y2 = 4x and x2 = 2y − 3 at the point (1, 2) ?
Write the angle between the curves y = e−x and y = ex at their point of intersections ?
Write the coordinates of the point at which the tangent to the curve y = 2x2 − x + 1 is parallel to the line y = 3x + 9 ?
The equation of the normal to the curve y = x(2 − x) at the point (2, 0) is ________________ .
The point on the curve y2 = x where tangent makes 45° angle with x-axis is ____________________ .
If the line y = x touches the curve y = x2 + bx + c at a point (1, 1) then _____________ .
The equation of the normal to the curve x = a cos3 θ, y = a sin3 θ at the point θ = π/4 is __________ .
Show that the equation of normal at any point on the curve x = 3cos θ – cos3θ, y = 3sinθ – sin3θ is 4 (y cos3θ – x sin3θ) = 3 sin 4θ
The point on the curve y2 = x, where the tangent makes an angle of `pi/4` with x-axis is ______.
Prove that the curves y2 = 4x and x2 + y2 – 6x + 1 = 0 touch each other at the point (1, 2)
The curve y = `x^(1/5)` has at (0, 0) ______.
If the curve ay + x2 = 7 and x3 = y, cut orthogonally at (1, 1), then the value of a is ______.
The distance between the point (1, 1) and the tangent to the curve y = e2x + x2 drawn at the point x = 0
The line y = x + 1 is a tangent to the curve y2 = 4x at the point
The normals to the curve x = a(θ + sinθ), y = a(1 – cosθ) at the points θ = (2n + 1)π, n∈I are all ______.
If the tangent to the conic, y – 6 = x2 at (2, 10) touches the circle, x2 + y2 + 8x – 2y = k (for some fixed k) at a point (α, β); then (α, β) is ______.
For the curve y2 = 2x3 – 7, the slope of the normal at (2, 3) is ______.
