Advertisements
Advertisements
प्रश्न
Find the points on the curve y = x3 at which the slope of the tangent is equal to the y-coordinate of the point.
उत्तर
The equation of the given curve is y = x3.
`:. dy/dx = 3x^2`
The slope of the tangent at the point (x, y) is given by,
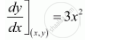
When the slope of the tangent is equal to the y-coordinate of the point, then y = 3x2.
Also, we have y = x3.
∴3x2 = x3
⇒ x2 (x − 3) = 0
⇒ x = 0, x = 3
When x = 0, then y = 0 and when x = 3, then y = 3(3)2 = 27.
Hence, the required points are (0, 0) and (3, 27).
APPEARS IN
संबंधित प्रश्न
Find the equations of the tangent and normal to the curve `x^2/a^2−y^2/b^2=1` at the point `(sqrt2a,b)` .
Find a point on the curve y = (x − 2)2 at which the tangent is parallel to the chord joining the points (2, 0) and (4, 4).
Find the equation of all lines having slope −1 that are tangents to the curve `y = 1/(x -1), x != 1`
Find the equations of the tangent and normal to the given curves at the indicated points:
y = x4 − 6x3 + 13x2 − 10x + 5 at (0, 5)
Find the equation of the normal at the point (am2, am3) for the curve ay2 = x3.
Find the points on the curve y = x3 − 2x2 − 2x at which the tangent lines are parallel to the line y = 2x− 3 ?
Find the points on the curve y2 = 2x3 at which the slope of the tangent is 3 ?
Find the point on the curve y = 3x2 + 4 at which the tangent is perpendicular to the line whose slop is \[- \frac{1}{6}\] ?
Find the points on the curve 2a2y = x3 − 3ax2 where the tangent is parallel to x-axis ?
Find the points on the curve \[\frac{x^2}{4} + \frac{y^2}{25} = 1\] at which the tangent is parallel to the x-axis ?
Find the equation of the tangent and the normal to the following curve at the indicated point y = x4 − 6x3 + 13x2 − 10x + 5 at x = 1?
Find the equation of the tangent and the normal to the following curve at the indicated point \[c^2 \left( x^2 + y^2 \right) = x^2 y^2 \text { at }\left( \frac{c}{\cos\theta}, \frac{c}{\sin\theta} \right)\] ?
Find the equation of the tangent and the normal to the following curve at the indicated point \[\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \text { at } \left( x_1 , y_1 \right)\] ?
Find the equation of the tangent to the curve x = θ + sin θ, y = 1 + cos θ at θ = π/4 ?
Find the equation of the normal to the curve x2 + 2y2 − 4x − 6y + 8 = 0 at the point whose abscissa is 2 ?
Find the equations of all lines having slope 2 and that are tangent to the curve \[y = \frac{1}{x - 3}, x \neq 3\] ?
At what points will be tangents to the curve y = 2x3 − 15x2 + 36x − 21 be parallel to x-axis ? Also, find the equations of the tangents to the curve at these points ?
Find the slope of the normal at the point 't' on the curve \[x = \frac{1}{t}, y = t\] ?
Write the equation on the tangent to the curve y = x2 − x + 2 at the point where it crosses the y-axis ?
Write the angle between the curves y2 = 4x and x2 = 2y − 3 at the point (1, 2) ?
The equation to the normal to the curve y = sin x at (0, 0) is ___________ .
If the tangent to the curve x = a t2, y = 2 at is perpendicular to x-axis, then its point of contact is _____________ .
The point at the curve y = 12x − x2 where the slope of the tangent is zero will be _____________ .
If the curve ay + x2 = 7 and x3 = y cut orthogonally at (1, 1), then a is equal to _____________ .
Any tangent to the curve y = 2x7 + 3x + 5 __________________ .
The slope of the tangent to the curve x = t2 + 3t − 8, y = 2t2 − 2t − 5 at the point (2, −1) is _____________ .
The line y = mx + 1 is a tangent to the curve y2 = 4x, if the value of m is ________________ .
Prove that the curves y2 = 4x and x2 + y2 – 6x + 1 = 0 touch each other at the point (1, 2)
If the straight line x cosα + y sinα = p touches the curve `x^2/"a"^2 + y^2/"b"^2` = 1, then prove that a2 cos2α + b2 sin2α = p2.
The curve y = `x^(1/5)` has at (0, 0) ______.
The equation of normal to the curve 3x2 – y2 = 8 which is parallel to the line x + 3y = 8 is ______.
For which value of m is the line y = mx + 1 a tangent to the curve y2 = 4x?
The point on the curves y = (x – 3)2 where the tangent is parallel to the chord joining (3, 0) and (4, 1) is ____________.
If `tan^-1x + tan^-1y + tan^-1z = pi/2`, then
The points at which the tangent passes through the origin for the curve y = 4x3 – 2x5 are
The normal at the point (1, 1) on the curve `2y + x^2` = 3 is
Two vertical poles of heights, 20 m and 80 m stand apart on a horizontal plane. The height (in meters) of the point of intersection of the lines joining the top of each pole to the foot of the other, From this horizontal plane is ______.
The curve `(x/a)^n + (y/b)^n` = 2, touches the line `x/a + y/b` = 2 at the point (a, b) for n is equal to ______.
