Advertisements
Advertisements
Question
Find the area of the region bounded by the curves (x -1)2 + y2 = 1 and x2 + y2 = 1, using integration.
Advertisements
Solution
The area bounded by the curves, (x – 1)2 + y2 = 1 and x2 + y 2 = 1, is represented by the shaded area as
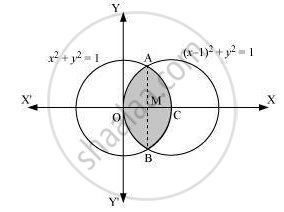
On solving the equations, (x – 1)2 + y2 = 1 and x2 + y 2 = 1, we obtain the point of intersection as A`(1/2, sqrt3/2) and B(1/2, -sqrt3/2)`
It can be observed that the required area is symmetrical about x-axis.
∴ Area OBCAO = 2 × Area OCAO
We join AB, which intersects OC at M, such that AM is perpendicular to OC.
The coordinates of M are `(1/2, 0)`.
⇒ Area OCAD = Area OMAO + Area MCAM
= `[ int_0^(1/2) sqrt(1 - (x - 1)^2) dx + int_(1/2)^1 sqrt(1 - x^2 ) dx ]`
= `[ (x -1)/2 sqrt(1 - (x - 1)^2) + 1/2 sin^-1(x -1)]_0^(1/2) + [ x/2 sqrt(1 - x)^2 + 1/2 sin^-1 x]_(1/2)^1`
= `[ - 1/4 sqrt( 1 - (-1/2)^2) + 1/2 sin^-1(1/2 - 1) - 1/2 sin^-1 (-1)] + [1/2 sin^-1 - 1/4 sqrt(1 - (1/2)^2) - 1/2sin^-1 (1/2)]`
= `[- sqrt3/8 + 1/2(- pi/6) - 1/2 (- pi/2)] + [1/2(pi/2) - sqrt3/8 - 1/2(pi/6)]`
= `[-sqrt3/4 - pi/12 + pi/4 + pi/4 - pi/12 ]`
= `[-sqrt3/4 - pi/6 + pi/2]`
= `[2pi/6 - sqrt3/4]`
Therefore, required area OBCAO = `2 xx (2pi/6 - sqrt3/4 ) = (2pi/3 - sqrt3/2)` units
APPEARS IN
RELATED QUESTIONS
Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.
Form the differential equation of the family of hyperbolas having foci on x-axis and centre at origin.
Show that the family of curves for which `dy/dx = (x^2+y^2)/(2x^2)` is given by x2 - y2 = cx
Form the differential equation of the family of curves represented by y2 = (x − c)3.
Form the differential equation from the following primitive where constants are arbitrary:
y2 = 4ax
Find the differential equation of the family of curves, x = A cos nt + B sin nt, where A and B are arbitrary constants.
Form the differential equation corresponding to y2 = a (b − x2) by eliminating a and b.
Form the differential equation corresponding to y2 − 2ay + x2 = a2 by eliminating a.
Form the differential equation of the family of curves represented by the equation (a being the parameter):
(2x − a)2 − y2 = a2
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
x2 + y2 = a2
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
x2 − y2 = a2
Represent the following families of curves by forming the corresponding differential equations (a, b being parameters):
x2 + y2 = ax3
Find one-parameter families of solution curves of the following differential equation:-
\[\left( x \log x \right)\frac{dy}{dx} + y = \log x\]
Find one-parameter families of solution curves of the following differential equation:-
\[\frac{dy}{dx} + y \cos x = e^{\sin x} \cos x\]
Find one-parameter families of solution curves of the following differential equation:-
\[\left( x + y \right)\frac{dy}{dx} = 1\]
Find one-parameter families of solution curves of the following differential equation:-
\[\frac{dy}{dx} \cos^2 x = \tan x - y\]
Find one-parameter families of solution curves of the following differential equation:-
\[e^{- y} \sec^2 y dy = dx + x dy\]
Find one-parameter families of solution curves of the following differential equation:-
\[x \log x\frac{dy}{dx} + y = 2 \log x\]
Form the differential equation representing the family of curves y = mx, where m is an arbitrary constant.
Find the differential equation of the family of curves y = Ae2x + B.e–2x.
Find the equation of a curve whose tangent at any point on it, different from origin, has slope `y + y/x`.
Find the equation of the curve through the point (1, 0) if the slope of the tangent to the curve at any point (x, y) is `(y - 1)/(x^2 + x)`
Find the equation of a curve passing through the point (1, 1). If the tangent drawn at any point P(x, y) on the curve meets the co-ordinate axes at A and B such that P is the mid-point of AB.
The differential equation `y ("d"y)/("d"x) + "c"` represents: ______.
The differential equation of the family of curves x2 + y2 – 2ay = 0, where a is arbitrary constant, is ______.
The differential equation representing the family of circles x2 + (y – a)2 = a2 will be of order two.
Differential equation representing the family of curves y = ex (Acosx + Bsinx) is `("d"^2y)/("d"x^2) - 2 ("d"y)/("d"x) + 2y` = 0
