Advertisements
Advertisements
Question
If 2 sin 2θ = `sqrt(3)` then the value of θ is
Options
90°
30°
45°
60°
Solution
30°
Explanation;
Hint:
2 sin 2θ = `sqrt(3)`
⇒ sin 2θ = `sqrt(3)/2`
sin 2θ = sin 60°
⇒ 2θ = 60°
θ = 30°
APPEARS IN
RELATED QUESTIONS
`(1- tan^2 45°)/(1+tan^2 45°)` = ______
Prove the following :
`(cos(90^@ - theta) sec(90^@ - theta)tan theta)/(cosec(90^@ - theta) sin(90^@ - theta) cot (90^@ - theta)) + tan (90^@ - theta)/cot theta = 2`
Prove the following
`(tan (90 - A) cot A)/(cosec^2 A) - cos^2 A =0`
Prove the following
sin (50° − θ) − cos (40° − θ) + tan 1° tan 10° tan 20° tan 70° tan 80° tan 89° = 1
Prove that
tan (55° − θ) − cot (35° + θ) = 0
ABC is an isosceles right-angled triangle. Assuming of AB = BC = x, find the value of each of the following trigonometric ratios: sin 45°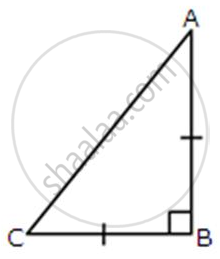
find the value of :
3sin2 30° + 2tan2 60° - 5cos2 45°
If A = 30°;
show that:
(sinA - cosA)2 = 1 - sin2A
If tan(A - B) = `(1)/sqrt(3)` and tan(A + B) = `sqrt(3)`, find A and B.
If sin α = `1/2`, then find the value of (3 cos α – 4 cos3 α).
