Advertisements
Advertisements
Question
If 49392 = a4b2c3, find the values of a, b and c, where a, b and c are different positive primes.
Solution
First find out the prime factorisation of 49392.
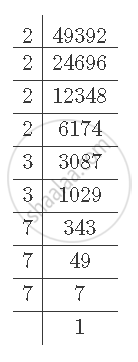
It can be observed that 49392 can be written as `2^4xx3^2xx7^3,` where 2, 3 and 7 are positive primes.
`therefore49392=2^4 3^2 7^3=a^4b^2c^3`
⇒ a = 2, b = 3, c = 7
APPEARS IN
RELATED QUESTIONS
Assuming that x, y, z are positive real numbers, simplify the following:
`(x^((-2)/3)y^((-1)/2))^2`
Simplify:
`(sqrt2/5)^8div(sqrt2/5)^13`
Show that:
`(3^a/3^b)^(a+b)(3^b/3^c)^(b+c)(3^c/3^a)^(c+a)=1`
If `x=2^(1/3)+2^(2/3),` Show that x3 - 6x = 6
Solve the following equation:
`sqrt(a/b)=(b/a)^(1-2x),` where a and b are distinct primes.
When simplified \[( x^{- 1} + y^{- 1} )^{- 1}\] is equal to
When simplified \[\left( - \frac{1}{27} \right)^{- 2/3}\] is
Which one of the following is not equal to \[\left( \sqrt[3]{8} \right)^{- 1/2} ?\]
`(2/3)^x (3/2)^(2x)=81/16 `then x =
If \[\frac{5 - \sqrt{3}}{2 + \sqrt{3}} = x + y\sqrt{3}\] , then
