Advertisements
Advertisements
प्रश्न
If 49392 = a4b2c3, find the values of a, b and c, where a, b and c are different positive primes.
उत्तर
First find out the prime factorisation of 49392.
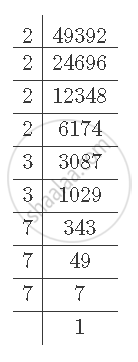
It can be observed that 49392 can be written as `2^4xx3^2xx7^3,` where 2, 3 and 7 are positive primes.
`therefore49392=2^4 3^2 7^3=a^4b^2c^3`
⇒ a = 2, b = 3, c = 7
APPEARS IN
संबंधित प्रश्न
If abc = 1, show that `1/(1+a+b^-1)+1/(1+b+c^-1)+1/(1+c+a^-1)=1`
Solve the following equation for x:
`2^(x+1)=4^(x-3)`
Solve the following equation for x:
`4^(2x)=1/32`
Assuming that x, y, z are positive real numbers, simplify the following:
`(x^-4/y^-10)^(5/4)`
Prove that:
`9^(3/2)-3xx5^0-(1/81)^(-1/2)=15`
Find the value of x in the following:
`2^(x-7)xx5^(x-4)=1250`
Write the value of \[\sqrt[3]{125 \times 27}\].
If a, b, c are positive real numbers, then \[\sqrt[5]{3125 a^{10} b^5 c^{10}}\] is equal to
If x is a positive real number and x2 = 2, then x3 =
\[\frac{5^{n + 2} - 6 \times 5^{n + 1}}{13 \times 5^n - 2 \times 5^{n + 1}}\] is equal to
