Advertisements
Advertisements
प्रश्न
If `1176=2^a3^b7^c,` find a, b and c.
उत्तर
First find out the prime factorisation of 1176.
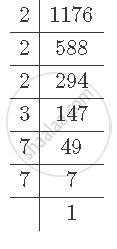
It can be observed that 1176 can be written as `2^3xx3^1xx7^2.`
`1176=2^3 3^1 7^2 = 2^a3^b7^c`
Hence, a = 3, b = 1 and c = 2.
APPEARS IN
संबंधित प्रश्न
Simplify the following
`(4ab^2(-5ab^3))/(10a^2b^2)`
Find the value of x in the following:
`(13)^(sqrtx)=4^4-3^4-6`
State the power law of exponents.
If (x − 1)3 = 8, What is the value of (x + 1)2 ?
If x = 2 and y = 4, then \[\left( \frac{x}{y} \right)^{x - y} + \left( \frac{y}{x} \right)^{y - x} =\]
If 9x+2 = 240 + 9x, then x =
If \[2^{- m} \times \frac{1}{2^m} = \frac{1}{4},\] then \[\frac{1}{14}\left\{ ( 4^m )^{1/2} + \left( \frac{1}{5^m} \right)^{- 1} \right\}\] is equal to
If x= \[\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}}\] and y = \[\frac{\sqrt{3} + \sqrt{2}}{\sqrt{3} - \sqrt{2}}\] , then x2 + y +y2 =
Simplify:
`(3/5)^4 (8/5)^-12 (32/5)^6`
Simplify:
`(9^(1/3) xx 27^(-1/2))/(3^(1/6) xx 3^(- 2/3))`
