Advertisements
Advertisements
प्रश्न
If `1176=2^a3^b7^c,` find a, b and c.
उत्तर
First find out the prime factorisation of 1176.
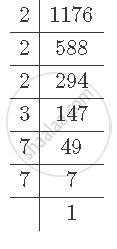
It can be observed that 1176 can be written as `2^3xx3^1xx7^2.`
`1176=2^3 3^1 7^2 = 2^a3^b7^c`
Hence, a = 3, b = 1 and c = 2.
APPEARS IN
संबंधित प्रश्न
Given `4725=3^a5^b7^c,` find
(i) the integral values of a, b and c
(ii) the value of `2^-a3^b7^c`
Simplify:
`(16^(-1/5))^(5/2)`
If ax = by = cz and b2 = ac, show that `y=(2zx)/(z+x)`
If `27^x=9/3^x,` find x.
For any positive real number x, write the value of \[\left\{ \left( x^a \right)^b \right\}^\frac{1}{ab} \left\{ \left( x^b \right)^c \right\}^\frac{1}{bc} \left\{ \left( x^c \right)^a \right\}^\frac{1}{ca}\]
The value of \[\left\{ 8^{- 4/3} \div 2^{- 2} \right\}^{1/2}\] is
The value of m for which \[\left[ \left\{ \left( \frac{1}{7^2} \right)^{- 2} \right\}^{- 1/3} \right]^{1/4} = 7^m ,\] is
If \[\frac{x}{x^{1 . 5}} = 8 x^{- 1}\] and x > 0, then x =
If \[x = 7 + 4\sqrt{3}\] and xy =1, then \[\frac{1}{x^2} + \frac{1}{y^2} =\]
If \[\sqrt{2} = 1 . 4142\] then \[\sqrt{\frac{\sqrt{2} - 1}{\sqrt{2} + 1}}\] is equal to
