Advertisements
Advertisements
प्रश्न
Given `4725=3^a5^b7^c,` find
(i) the integral values of a, b and c
(ii) the value of `2^-a3^b7^c`
उत्तर
(i) Given `4725=3^a5^b7^c`
First find out the prime factorisation of 4725.
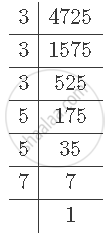
It can be observed that 4725 can be written as `3^3xx5^2xx7^1.`
`therefore4725 = 3^a5^b7^c=3^3 5^2 7^1`
Hence, a = 3, b = 2 and c = 1.
(ii)
When a = 3, b = 2 and c = 1,
`2^-a3^b7^c`
`=2^-3xx3^2xx7^1`
`=1/8xx9xx7`
`=63/8`
APPEARS IN
संबंधित प्रश्न
Solve the following equation for x:
`7^(2x+3)=1`
Assuming that x, y, z are positive real numbers, simplify the following:
`(sqrtx)^((-2)/3)sqrt(y^4)divsqrt(xy^((-1)/2))`
Find the value of x in the following:
`(2^3)^4=(2^2)^x`
For any positive real number x, write the value of \[\left\{ \left( x^a \right)^b \right\}^\frac{1}{ab} \left\{ \left( x^b \right)^c \right\}^\frac{1}{bc} \left\{ \left( x^c \right)^a \right\}^\frac{1}{ca}\]
The product of the square root of x with the cube root of x is
If a, b, c are positive real numbers, then \[\sqrt[5]{3125 a^{10} b^5 c^{10}}\] is equal to
The value of m for which \[\left[ \left\{ \left( \frac{1}{7^2} \right)^{- 2} \right\}^{- 1/3} \right]^{1/4} = 7^m ,\] is
If x= \[\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}}\] and y = \[\frac{\sqrt{3} + \sqrt{2}}{\sqrt{3} - \sqrt{2}}\] , then x2 + y +y2 =
The value of \[\frac{\sqrt{48} + \sqrt{32}}{\sqrt{27} + \sqrt{18}}\] is
Which of the following is equal to x?
