Advertisements
Advertisements
Question
Given `4725=3^a5^b7^c,` find
(i) the integral values of a, b and c
(ii) the value of `2^-a3^b7^c`
Solution
(i) Given `4725=3^a5^b7^c`
First find out the prime factorisation of 4725.
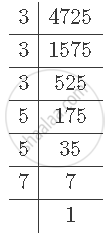
It can be observed that 4725 can be written as `3^3xx5^2xx7^1.`
`therefore4725 = 3^a5^b7^c=3^3 5^2 7^1`
Hence, a = 3, b = 2 and c = 1.
(ii)
When a = 3, b = 2 and c = 1,
`2^-a3^b7^c`
`=2^-3xx3^2xx7^1`
`=1/8xx9xx7`
`=63/8`
APPEARS IN
RELATED QUESTIONS
Simplify the following:
`(5^(n+3)-6xx5^(n+1))/(9xx5^x-2^2xx5^n)`
Assuming that x, y, z are positive real numbers, simplify the following:
`(x^((-2)/3)y^((-1)/2))^2`
If 3x = 5y = (75)z, show that `z=(xy)/(2x+y)`
Determine `(8x)^x,`If `9^(x+2)=240+9^x`
Simplify:
`root(lm)(x^l/x^m)xxroot(mn)(x^m/x^n)xxroot(nl)(x^n/x^l)`
Write the value of \[\left\{ 5( 8^{1/3} + {27}^{1/3} )^3 \right\}^{1/4} . \]
If \[\frac{3^{5x} \times {81}^2 \times 6561}{3^{2x}} = 3^7\] then x =
The value of \[\sqrt{5 + 2\sqrt{6}}\] is
Find:-
`125^(1/3)`
If `a = 2 + sqrt(3)`, then find the value of `a - 1/a`.
