Advertisements
Advertisements
प्रश्न
Given `4725=3^a5^b7^c,` find
(i) the integral values of a, b and c
(ii) the value of `2^-a3^b7^c`
उत्तर
(i) Given `4725=3^a5^b7^c`
First find out the prime factorisation of 4725.
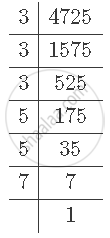
It can be observed that 4725 can be written as `3^3xx5^2xx7^1.`
`therefore4725 = 3^a5^b7^c=3^3 5^2 7^1`
Hence, a = 3, b = 2 and c = 1.
(ii)
When a = 3, b = 2 and c = 1,
`2^-a3^b7^c`
`=2^-3xx3^2xx7^1`
`=1/8xx9xx7`
`=63/8`
APPEARS IN
संबंधित प्रश्न
Simplify the following
`((x^2y^2)/(a^2b^3))^n`
If abc = 1, show that `1/(1+a+b^-1)+1/(1+b+c^-1)+1/(1+c+a^-1)=1`
Assuming that x, y, z are positive real numbers, simplify the following:
`(sqrt(x^-3))^5`
Prove that:
`9^(3/2)-3xx5^0-(1/81)^(-1/2)=15`
If `x=2^(1/3)+2^(2/3),` Show that x3 - 6x = 6
Solve the following equation:
`3^(x+1)=27xx3^4`
Solve the following equation:
`4^(x-1)xx(0.5)^(3-2x)=(1/8)^x`
Write \[\left( \frac{1}{9} \right)^{- 1/2} \times (64 )^{- 1/3}\] as a rational number.
Which one of the following is not equal to \[\left( \frac{100}{9} \right)^{- 3/2}\]?
Find:-
`125^(1/3)`
