Advertisements
Advertisements
प्रश्न
If 49392 = a4b2c3, find the values of a, b and c, where a, b and c are different positive primes.
उत्तर
First find out the prime factorisation of 49392.
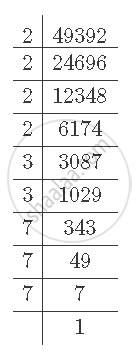
It can be observed that 49392 can be written as `2^4xx3^2xx7^3,` where 2, 3 and 7 are positive primes.
`therefore49392=2^4 3^2 7^3=a^4b^2c^3`
⇒ a = 2, b = 3, c = 7
APPEARS IN
संबंधित प्रश्न
If a = 3 and b = -2, find the values of :
ab + ba
Solve the following equations for x:
`3^(2x+4)+1=2.3^(x+2)`
Show that:
`(x^(1/(a-b)))^(1/(a-c))(x^(1/(b-c)))^(1/(b-a))(x^(1/(c-a)))^(1/(c-b))=1`
Find the value of x in the following:
`(root3 4)^(2x+1/2)=1/32`
Simplify \[\left[ \left\{ \left( 625 \right)^{- 1/2} \right\}^{- 1/4} \right]^2\]
If g = `t^(2/3) + 4t^(-1/2)`, what is the value of g when t = 64?
\[\frac{5^{n + 2} - 6 \times 5^{n + 1}}{13 \times 5^n - 2 \times 5^{n + 1}}\] is equal to
The simplest rationalising factor of \[\sqrt{3} + \sqrt{5}\] is ______.
If x= \[\frac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}}\] and y = \[\frac{\sqrt{3} + \sqrt{2}}{\sqrt{3} - \sqrt{2}}\] , then x2 + y +y2 =
Simplify:
`(3/5)^4 (8/5)^-12 (32/5)^6`
