Advertisements
Advertisements
Question
If one diagonal of a square is along the line 8x – 15y = 0 and one of its vertex is at (1, 2), then find the equation of sides of the square passing through this vertex.
Solution
Let ABCD be the given square and the coordinates of the vertex D be (1, 2).
We are required to find the equations of its sides DC and AD.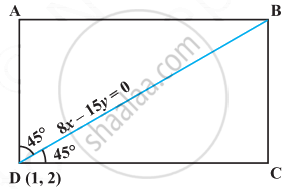
Given that BD is along the line 8x – 15y = 0, so its slope is `8/15` (Why?).
The angles made by BD with sides AD and DC is 45° (Why?).
Let the slope of DC be m.
Then tan 45° = `(m - 8/15)/(1 + (8m)/15)` (Why?)
or 15 + 8m = 15m – 8
or 7m = 23, which gives m = `23/7`
Therefore, the equation of the side DC is given by
y – 2 = `23/7 (x - 1)` or 23x – 7y – 9 = 0.
Similarly, the equation of another side AD is given by
y – 2 = `(-7)/23 (x - 1)` or 7x + 23y – 53 = 0.
APPEARS IN
RELATED QUESTIONS
Find the values of k for which the line (k–3) x – (4 – k2) y + k2 –7k + 6 = 0 is
- Parallel to the x-axis,
- Parallel to the y-axis,
- Passing through the origin.
Find the slope of the lines which make the following angle with the positive direction of x-axis:
\[\frac{2\pi}{3}\]
Find the slope of a line passing through the following point:
\[(a t_1^2 , 2 a t_1 ) \text { and } (a t_2^2 , 2 a t_2 )\]
State whether the two lines in each of the following is parallel, perpendicular or neither.
Through (3, 15) and (16, 6); through (−5, 3) and (8, 2).
What can be said regarding a line if its slope is positive ?
Without using the distance formula, show that points (−2, −1), (4, 0), (3, 3) and (−3, 2) are the vertices of a parallelogram.
Find the angle between X-axis and the line joining the points (3, −1) and (4, −2).
Find the equation of a line which is perpendicular to the line joining (4, 2) and (3, 5) and cuts off an intercept of length 3 on y-axis.
Find the equation of the right bisector of the line segment joining the points (3, 4) and (−1, 2).
The line through (h, 3) and (4, 1) intersects the line 7x − 9y − 19 = 0 at right angle. Find the value of h.
Find the angles between the following pair of straight lines:
3x + y + 12 = 0 and x + 2y − 1 = 0
Find the angles between the following pair of straight lines:
3x − y + 5 = 0 and x − 3y + 1 = 0
Find the angles between the following pair of straight lines:
x − 4y = 3 and 6x − y = 11
Find the acute angle between the lines 2x − y + 3 = 0 and x + y + 2 = 0.
If θ is the angle which the straight line joining the points (x1, y1) and (x2, y2) subtends at the origin, prove that \[\tan \theta = \frac{x_2 y_1 - x_1 y_2}{x_1 x_2 + y_1 y_2}\text { and } \cos \theta = \frac{x_1 x_2 + y_1 y_2}{\sqrt{{x_1}^2 + {y_1}^2}\sqrt{{x_2}^2 + {y_2}^2}}\].
Prove that the straight lines (a + b) x + (a − b ) y = 2ab, (a − b) x + (a + b) y = 2ab and x + y = 0 form an isosceles triangle whose vertical angle is 2 tan−1 \[\left( \frac{a}{b} \right)\].
Show that the line a2x + ay + 1 = 0 is perpendicular to the line x − ay = 1 for all non-zero real values of a.
Show that the tangent of an angle between the lines \[\frac{x}{a} + \frac{y}{b} = 1 \text { and } \frac{x}{a} - \frac{y}{b} = 1\text { is } \frac{2ab}{a^2 - b^2}\].
If m1 and m2 are slopes of lines represented by 6x2 - 5xy + y2 = 0, then (m1)3 + (m2)3 = ?
If the line joining two points A(2, 0) and B(3, 1) is rotated about A in anticlock wise direction through an angle of 15°. Find the equation of the line in new position.
If the slope of a line passing through the point A(3, 2) is `3/4`, then find points on the line which are 5 units away from the point A.
The reflection of the point (4, – 13) about the line 5x + y + 6 = 0 is ______.
Equation of the line passing through (1, 2) and parallel to the line y = 3x – 1 is ______.
Equations of the lines through the point (3, 2) and making an angle of 45° with the line x – 2y = 3 are ______.
A ray of light coming from the point (1, 2) is reflected at a point A on the x-axis and then passes through the point (5, 3). The co-ordinates of the point A is ______.
