Advertisements
Advertisements
Question
Measure the length of the floor of your classroom in meters. Also measure the width.
- If you want to move around easily then how many children do you think should be there in one square meter?
Solution
Two children.
APPEARS IN
RELATED QUESTIONS
Let ABCD be a parallelogram of area 124 cm2. If E and F are the mid-points of sides AB and
CD respectively, then find the area of parallelogram AEFD.
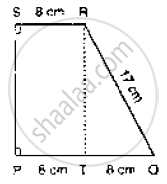
Compute the area of trapezium PQRS is Fig. below.
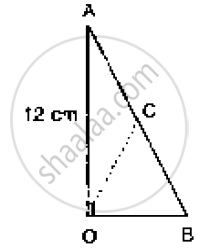
In the below fig. ∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm. Find the area of
ΔAOB.
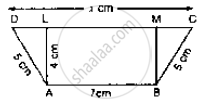
In the below fig. ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm,
and distance between AB and DC is 4cm. Find the value of x and area of trapezium ABCD.
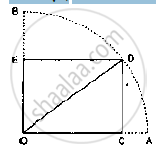
In the below fig. OCDE is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If
OE = 2√5, find the area of the rectangle.
A point D is taken on the side BC of a ΔABC such that BD = 2DC. Prove that ar(Δ ABD) =
2ar (ΔADC).
ABCD is a parallelogram. E is a point on BA such that BE = 2 EA and F is a point on DC
such that DF = 2 FC. Prove that AE CF is a parallelogram whose area is one third of the
area of parallelogram ABCD.
In the given figure, ABCD is a rectangle in which CD = 6 cm, AD = 8 cm. Find the area of parallelogram CDEF.

PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm. A is any point on PQ. If PS = 5 cm, then find ar (ΔRAS)
In a ΔABC, D, E, F are the mid-points of sides BC, CA and AB respectively. If ar (ΔABC) = 16cm2, then ar (trapezium FBCE) =
The area of the figure formed by joining the mid-points of the adjacent sides of a rhombus with diagonals 16 cm and 12 cm is
A, B, C, D are mid-points of sides of parallelogram PQRS. If ar (PQRS) = 36 cm2, then ar (ABCD) =
If AD is median of ΔABC and P is a point on AC such that
ar (ΔADP) : ar (ΔABD) = 2 : 3, then ar (Δ PDC) : ar (Δ ABC)
ABCD is a trapezium in which AB || DC. If ar (ΔABD) = 24 cm2 and AB = 8 cm, then height of ΔABC is
The medians of a triangle ABC intersect each other at point G. If one of its medians is AD,
prove that:
(i) Area ( ΔABD ) = 3 x Area ( ΔBGD )
(ii) Area ( ΔACD ) = 3 x Area ( ΔCGD )
(iii) Area ( ΔBGC ) = `1/3` x Area ( ΔABC ).
The diagonal of a rectangular board is 1 m and its length is 96 cm. Find the area of the board.
Find the area of a rectangle whose length = 3.6 m breadth = 90 cm
Find the area of a square, whose side is: 4.5 cm.
What will happen to the area of a rectangle, if its length and breadth both are trebled?
Length of a rectangle is 30 m and its breadth is 20 m. Find the increase in its area if its length is increased by 10 m and its breadth is doubled.
The table given below contains some measures of the rectangle. Find the unknown values.
| Length | Breadth | Perimeter | Area |
| ? | 15 cm | 60 cm | ? |
So the area of piece A = ________ square cm
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- A shopkeeper has 204 eggs. He puts them in egg trays. Each tray has 12 eggs.
a) How many more eggs will he need? b) How many fresh eggs does he sell? c) How many egg trays does he need?
Each line gives a story. You have to choose the question which makes the best story problem. The first one is already marked.
- The cost of one book is Rs 47. Sonu buys 23 books.
a) How much money does she have? b) How much money does she pay for the books? c) What is the cost of 47 books?
Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

Find the area of the following figure by counting squares:

