Advertisements
Advertisements
Question
Prove `tan^(-1) 1/5 + tan^(-1) (1/7) + tan^(-1) 1/3 + tan^(-1) 1/8 = pi/4`
Solution
L.H.S = `tan^(-1) 1/5 + tan^(-1) 1/7 + tan^(-1) 1/3 + tan^(-1) 1/8`
= `tan^(-1) ((1/5 + 1/7)/(1-1/5 xx 1/7)) + tan^(-1) ((1/3 + 1/8)/(1-1/3 xx 1/8))` `" "[tan^(-1) x + tan^(-1) y = tan^(-1) (x + y)/(1 - xy)]`
`= tan^(-1) ((7+5)/(35-1)) + tan^(-1) ((8 + 3)/(24 - 1))`
`= tan^(-1) 12/34 + tan^(-1) 11/23`
= `tan^(-1) ((6/17 + 11/23 )/(1- 6/17 xx 11/23))`
`= tan^(-1) ((138 + 187)/(391 - 66))`
`= tan^(-1) (325/325) = tan^(-1) `
`= pi/4` = R.H.S
APPEARS IN
RELATED QUESTIONS
Write the function in the simplest form: `tan^(-1) 1/(sqrt(x^2 - 1)), |x| > 1`
Write the following function in the simplest form:
`tan^(-1) ((3a^2 x - x^3)/(a^3 - 3ax^2)), a > 0; (-a)/sqrt3 <= x a/sqrt3`
Find the value of following:
`tan 1/2 [sin^(-1) (2x)/(1+ x^2) + cos^(-1) (1-y^2)/(1+y^2)], |x| < 1, y> 0 and xy < 1`
Find the value of the given expression.
`tan^(-1) (tan (3pi)/4)`
`cos^(-1) (cos (7pi)/6)` is equal to ______.
`sin[pi/3 - sin^(-1) (-1/2)]` is equal to ______.
Prove that:
`tan^(-1) sqrtx = 1/2 cos^(-1) ((1-x)/(1+x)) , x in [0, 1]`
sin–1 (1 – x) – 2 sin–1 x = `pi/2` , then x is equal to ______.
Solve the following equation for x: `cos (tan^(-1) x) = sin (cot^(-1) 3/4)`
If tan-1 x - cot-1 x = tan-1 `(1/sqrt(3)),`x> 0 then find the value of x and hence find the value of sec-1 `(2/x)`.
Find: ∫ sin x · log cos x dx
Solve: tan-1 4 x + tan-1 6x `= π/(4)`.
Find the value of `sin^-1[cos(sin^-1 (sqrt(3)/2))]`
Solve: `2tan^-1 (cos x) = tan^-1 (2"cosec" x)`
Solve: `cot^-1 x - cot^-1 (x + 2) = pi/12, x > 0`
Choose the correct alternative:
`sin^-1 3/5 - cos^-1 13/13 + sec^-1 5/3 - "cosec"^-1 13/12` is equal to
Choose the correct alternative:
If `sin^-1x + cot^-1 (1/2) = pi/2`, then x is equal to
Prove that `2sin^-1 3/5 - tan^-1 17/31 = pi/4`
Show that `2tan^-1 {tan alpha/2 * tan(pi/4 - beta/2)} = tan^-1 (sin alpha cos beta)/(cosalpha + sinbeta)`
If `tan^-1x = pi/10` for some x ∈ R, then the value of cot–1x is ______.
If 3 tan–1x + cot–1x = π, then x equals ______.
The value of the expression `tan (1/2 cos^-1 2/sqrt(5))` is ______.
The value of `"tan"^-1 (1/2) + "tan"^-1 (1/3) + "tan"^-1 (7/8)` is ____________.
The value of expression 2 `"sec"^-1 2 + "sin"^-1 (1/2)`
`"cos" (2 "tan"^-1 1/7) - "sin" (4 "sin"^-1 1/3) =` ____________.
If tan-1 2x + tan-1 3x = `pi/4,` then x is ____________.
If `"tan"^-1 (("x" - 1)/("x" + 2)) + "tan"^-1 (("x" + 1)/("x" + 2)) = pi/4,` then x is equal to ____________.
The value of cot-1 9 + cosec-1 `(sqrt41/4)` is given by ____________.
The value of `"cos"^-1 ("cos" ((33pi)/5))` is ____________.
`"tan"^-1 1 + "cos"^-1 ((-1)/2) + "sin"^-1 ((-1)/2)`
`"sin"^-1 ((-1)/2)`
The Government of India is planning to fix a hoarding board at the face of a building on the road of a busy market for awareness on COVID-19 protocol. Ram, Robert and Rahim are the three engineers who are working on this project. “A” is considered to be a person viewing the hoarding board 20 metres away from the building, standing at the edge of a pathway nearby. Ram, Robert and Rahim suggested to the firm to place the hoarding board at three different locations namely C, D and E. “C” is at the height of 10 metres from the ground level. For viewer A, the angle of elevation of “D” is double the angle of elevation of “C” The angle of elevation of “E” is triple the angle of elevation of “C” for the same viewer. Look at the figure given and based on the above information answer the following:
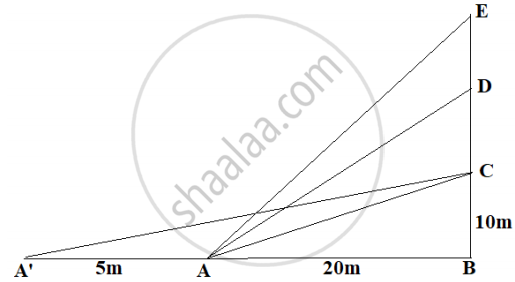
Measure of ∠CAB = ________.
The Government of India is planning to fix a hoarding board at the face of a building on the road of a busy market for awareness on COVID-19 protocol. Ram, Robert and Rahim are the three engineers who are working on this project. “A” is considered to be a person viewing the hoarding board 20 metres away from the building, standing at the edge of a pathway nearby. Ram, Robert and Rahim suggested to the firm to place the hoarding board at three different locations namely C, D and E. “C” is at the height of 10 metres from the ground level. For viewer A, the angle of elevation of “D” is double the angle of elevation of “C” The angle of elevation of “E” is triple the angle of elevation of “C” for the same viewer. Look at the figure given and based on the above information answer the following:

𝐴' Is another viewer standing on the same line of observation across the road. If the width of the road is 5 meters, then the difference between ∠CAB and ∠CA'B is ______.
What is the value of cos (sec–1x + cosec–1x), |x| ≥ 1
`50tan(3tan^-1(1/2) + 2cos^-1(1/sqrt(5))) + 4sqrt(2) tan(1/2tan^-1(2sqrt(2)))` is equal to ______.
Write the following function in the simplest form:
`tan^-1 ((cos x - sin x)/(cos x + sin x)), (-pi)/4 < x < (3 pi)/4`
